圆锥曲线的切线方程及其性质
一、椭圆的切线方程
我们先求椭圆的割线方程。设有椭圆 \(\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1\) 。取椭圆上两点 (\(x_0\), \(y_0\)),(\(x_1\), \(y_1\)), 则过两点的割线方程可表示为
\[y - y_0 = \dfrac{y_1 - y_0}{x_1 - x_0} (x - x_0) = \dfrac{y_1^2 - y_0^2}{(x_1 - x_0)(y_1 + y_0)} (x - x_0) \]利用 \(y_0^2\) = \(b^2\) - \(\dfrac{b^2}{a^2}\) \(x_0^2\), \(y_1^2\) = \(b^2\) - \(\dfrac{b^2}{a^2}\) \(x_1^2\),我们可以化简得到
\[y - y_0 = -\dfrac{b^2}{a^2} \dfrac{x_1 + x_0}{y_1 + y_0} (x - x_0) \]令 \(y_1\) = \(y_0\) , \(x_1\) = \(x_0\), 即可得到椭圆的切线方程
\[y - y_0 = -\dfrac{b^2 x_0}{a^2 y_0} (x - x_0) \]整理得
\[\dfrac{x_0 x}{a^2} + \dfrac{y_0 y}{b^2} = 1 \]二、圆锥曲线的切线方程
经圆锥曲线上一点(\(x_0\), \(y_0\))的切线方程为
\[\text{椭圆 } \dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1 \Rightarrow \dfrac{x_0 x}{a^2} + \dfrac{y_0 y}{b^2} = 1 \]\[\text{双曲线 } \dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1 \Rightarrow \dfrac{x_0 x}{a^2} - \dfrac{y_0 y}{b^2} = 1 \]\[\text{抛物线 } y^2 = 2px \Rightarrow y_0 y = p(x + x_0) \]不难发现,对于圆锥曲线的切线方程,有以下代换规则
\[x_0 x \rightarrow x^2, y_0 y \rightarrow y^2 \]\[\dfrac{x_0 + x}{2} \rightarrow x,\dfrac{y_0 y}{2} \rightarrow y \]三、圆锥曲线的切线相关性质
- 双曲线的两条渐近线所夹的切线段被切点平分。
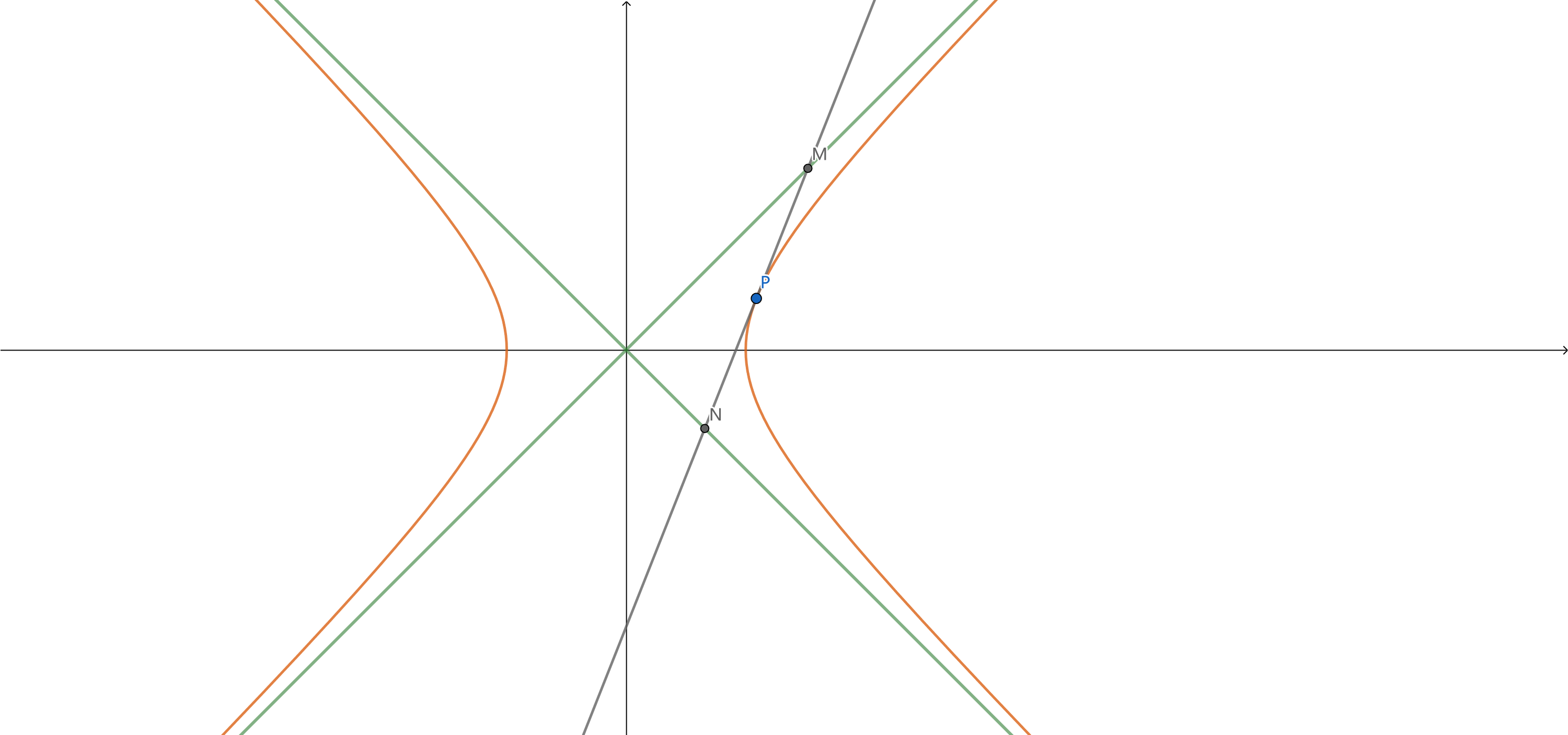
如图,P (\(x_0\), \(y_0\)) 为双曲线 \(\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1\) 上一点,与双曲线的渐近线 y = \(\pm\) \(\dfrac{b}{a}\)x 相交于 M, N 两点,则 P 为 MN 的中点。
证明如下:
过点 P 的切线方程为 \(\dfrac{x_0 x}{a^2} - \dfrac{y_0 y}{b^2} = 1\),与双曲线的渐近线 y = \(\pm\) \(\dfrac{b}{a}\)x 相交于
\[M(\dfrac{a^2 b}{b x_0 - a y_0}, \dfrac{a b^2}{b x_0 - a y_0}), N(\dfrac{a^2 b}{b x_0 + a y_0}, \dfrac{a b^2}{b x_0 + a y_0}) \]易得 P(\(x_0\), \(y_0\)) 为线段 MN 的中点
-
圆锥曲线的光学性质
-
过椭圆上一点的切线的垂线(即法线)平分过该点的两条焦半径的夹角。
-
过双曲线上一点的切线的垂线(即法线)平分过该点的两条焦半径的夹角的补角。
-
过抛物线上一点的切线的垂线(即法线)平分过该点的焦半径与过该点且平行于对称轴的直线的夹角。
-
以下给出性质 1 的证明。
欲证明两角相等,我们可以借助平面向量。
过椭圆上一点 P(\(x_0\),\(y_0\)) 的切线方程为 \(\dfrac{x_0 x}{a^2} + \dfrac{y_0 y}{b^2} = 1\)
因此过该点的法线的方向向量 \(\vec{n} = (b^2 x_0, a^2 y_0)\)
又 \(\vec{F_1 P} = (x_0 + c, y)\), \(\vec{F_2 P} = (x_0 - c, y)\), 且 |\(\vec{F_1 P}\)| = a + e\(x_0\), |\(\vec{F_2 P}\)| = a - e\(x_0\)
所以
\[\cos <\vec{F_1 P}, \vec{n}> = \dfrac{(b^2 x_0^2 + a^2 y_0^2) + b^2 c x_0}{\dfrac{a^2 + c x_0}{a} |\vec{n}|} = \dfrac{(a^2 + c x_0) b^2}{\dfrac{a^2 + c x_0}{a} |\vec{n}|} = \dfrac{a b^2}{|\vec{n}|} \]\[\cos <\vec{F_2 P}, \vec{n}> = \dfrac{(b^2 x_0^2 + a^2 y_0^2) - b^2 c x_0}{\dfrac{a^2 - c x_0}{a} |\vec{n}|} = \dfrac{(a^2 - c x_0) b^2}{\dfrac{a^2 - c x_0}{a} |\vec{n}|} = \dfrac{a b^2}{|\vec{n}|} \]故 <\(\vec{F_1 P}, \vec{n}\)> = <\(\vec{F_2 P}, \vec{n}\)>
该性质揭示了椭圆的光学性质:从椭圆一焦点发出的光线其反射光线经过另一个焦点。
标签:方程,椭圆,切线,dfrac,vec,圆锥曲线 来源: https://www.cnblogs.com/sunirein/p/16455592.html
本站声明: 1. iCode9 技术分享网(下文简称本站)提供的所有内容,仅供技术学习、探讨和分享; 2. 关于本站的所有留言、评论、转载及引用,纯属内容发起人的个人观点,与本站观点和立场无关; 3. 关于本站的所有言论和文字,纯属内容发起人的个人观点,与本站观点和立场无关; 4. 本站文章均是网友提供,不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属;如您发现该文章侵犯了您的权益,可联系我们第一时间进行删除; 5. 本站为非盈利性的个人网站,所有内容不会用来进行牟利,也不会利用任何形式的广告来间接获益,纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。
