随机事件及其概率
一. 概率的基本定义及性质
-
试验E中每一个可能结果称为基本事件,或称为样本点
-
所有基本事件组成的集合称为试验E的样本空间,即为\(\Omega\)
-
两种特殊事件: 必然事件\(\Omega\)(概率为1),不可能事件 \(\empty\) (概率为0)
-
事件运算:
-
包含: 事件A发生必然导致事件B发生,则称事件B包含事件A
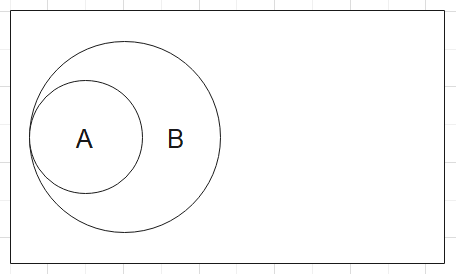
\(B \supset A ; A \subset B\)
显然\(\Omega \supset A \supset \empty\)
-
相等:
$A \subset B $且 \(B \subset A\)则\(A = B\)
-
并:
\(A \cup B\)
-
交:
\(A \cap B\)
-
差:
\(A - B = A \cap \neg B = A \cap \overline{B}\)
-
不相容:
\(A\cap B = \empty\)
-
对立:
$A \cap B = \empty $ 且 \(A + B = \Omega\)
对立一定不相容,不相容不一定对立
-
-
常用运算律:
-
交换律
\(A \cup B = B \cup A \\ A \cap B = B \cap A\)
-
结合律
\((A \cup B ) \cup C = A \cup (B\cup C) \\ (A \cap B )\cap C = A \cap( B \cap C)\)
-
分配律
\(A \cup (B \cap C) = (A \cup B) \cap (B \cup C) \\ A \cap(B \cup C) = (A \cap B) \cup (B \cap C)\)
-
反演律
\(\overline{A \cap B} = \overline{A} \cup \overline{B} \\ \overline{A \cup B} = \overline{A} \cap \overline{B}\)
-
-
概率公理化
- 非负性: 对于任何一个事件A,\(P(A) \geqslant 0\)
- 规范性: \(P(\Omega) = 1\)
- 可列可加性: 对于两两不相容事件\(P(\sum_{i=1}^{\infin} A_i) = \sum_{i=1}^{\infin}A_i\)
推论性质:
- \(P(\empty) = 0\)
- 有限可加性: 若事件\(A_1,A_2,...,A_n\)两两不相容,则\(P(A_1+A_2+A_3+...+A_n) = P(A_1) + P(A_2) + ... + P(A_n)\)
- 可减性: 若\(B \supset A,\)则 \(P(B - A) = P(B) - P(A)\)
- 单调性:若\(B \supset A,\)则\(P(B) \geqslant P(A)\)
- \(P(A) + P(\overline{A}) = 1\)
- 加法公式: \(P(A\cup B) = P(A) + P(B) - P(AB)\)
二.条件概率与事件独立性
-
条件概率:在事件A发生的条件下事件B发生的概率: \(P(B|A) = \frac{P(AB)}{P(A)}\)
-
乘法公式: \(P(AB) = P(A) * P(B|A)\)
乘法公式:\(P(A_1A_2...A_n) = P(A_1) * P(A_2|A_1) * P(A_3| A_1A_2) ... P(A_n | A_1A_2...A_{n-1})\)
记忆方法: 这是一个逐步构造\(P(A_1A_2...A_n)\)的过程,先用乘法公式构造\(P(A_1A_2)\), 再用乘法公式构造\(P(A_1A_2A_3)\),....,最后构造\(P(A_1A_2...A_n)\)
-
事件独立性: 事件A,B满足\(P(AB) = P(A) * P(B)\)则称事件A,B独立. 因为此时有\(P(A) = P(A|B), P(B) = P(B|A)\)
-
n事件独立性: 对于任意规模的部分子集S,S中元素任意取自\(A_1,A_2,...A_n\),都有\(P(A_{r1},A_{r2},...A_{rk}) = P(A_{r1})P(A_{r2})...P_{rk}\)
-
全概率公式:
设\(A_1,A_2,...,A_n\)是概率空间的一组事件,若它们两两互不相容,而且\(\sum_{k=1}^{n}A_k = \Omega\)
则称\(A_1,A_2,...,A_n\)是样本空间\(\Omega\)的一个分割,亦称为完备事件组
全概率公式是加法公式和乘法公式的组合:
\(P(B) = \sum_{k=1}^n P(A_k) P(B|A_k)\)
证明: \(P(B) = P(B\Omega) = P(B) * P(\Omega) = P(B) * (P(A_1) + P(A_2) + ... + P(A_n)) = \sum_{k=1}^nP(BA_k) = \sum_{k=1}^n P(A_k) * P(B|A_k)\)
事件B发生的概率是各个"原因"下的条件概率的加权平均
-
贝叶斯公式:
贝叶斯公式是全概率公式和条件概率公式的组合:
\(P(A_k|B) = \frac{P(A_kB)}{P(B)} = \frac{P(A_k)P(B|A_k)}{\sum_{j=1}^nP(A_j)P(B|A_j)}\)
三种概型
-
古典概型:
试验结果共有n个基本事件,且各个基本事件等可能,事件A由m个基本事件组成,则\(P(A) = \frac{m}{n}\)
-
几何概型:
试验结果的每一个基本事件可以几何表示为某个区域中的点,则\(P(A) = \frac{A的测度}{\Omega的测度}\)
-
伯努利概型:
如果试验E的可能结果为两个:\(A\)及\(\overline{A}\),则称试验E为伯努利试验; 若将试验E重复n次,则称为n重伯努利试验
在n重伯努利试验中,事件A发生的概率为p,则A发生k次的概率为
\(P_n(k) = C_{n}^kp^k(1-p)^{n-k}\)
标签:...,概率,cup,cap,随机,Omega,事件 来源: https://www.cnblogs.com/popodynasty/p/13944745.html
本站声明: 1. iCode9 技术分享网(下文简称本站)提供的所有内容,仅供技术学习、探讨和分享; 2. 关于本站的所有留言、评论、转载及引用,纯属内容发起人的个人观点,与本站观点和立场无关; 3. 关于本站的所有言论和文字,纯属内容发起人的个人观点,与本站观点和立场无关; 4. 本站文章均是网友提供,不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属;如您发现该文章侵犯了您的权益,可联系我们第一时间进行删除; 5. 本站为非盈利性的个人网站,所有内容不会用来进行牟利,也不会利用任何形式的广告来间接获益,纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。
