ICode9
精准搜索请尝试： 精确搜索
首页
编程语言>
数据库
系统相关
互联网
其他分享
Python
Java
JavaScript
android
PHP
首页 > 其他分享> 文章详细

树链剖分入门

2020-06-25 20:51:32  阅读：224  来源： 互联网

标签：入门 剖分 int top dfs 树链 leq son 节点


又是一个美妙的算法

定义

  • 重儿子：在一个点 \(x\) 的子节点中，拥有最大子树的儿子 \(y\) 是 \(x\) 的重儿子。
  • 轻儿子：在一个点 \(x\) 的子节点中，除去重儿子的子节点为 \(x\) 的轻儿子。
  • 重边：父亲与重儿子的连边。
  • 轻边：父亲与轻儿子的连边。
  • 重链：只由重边构成的链。

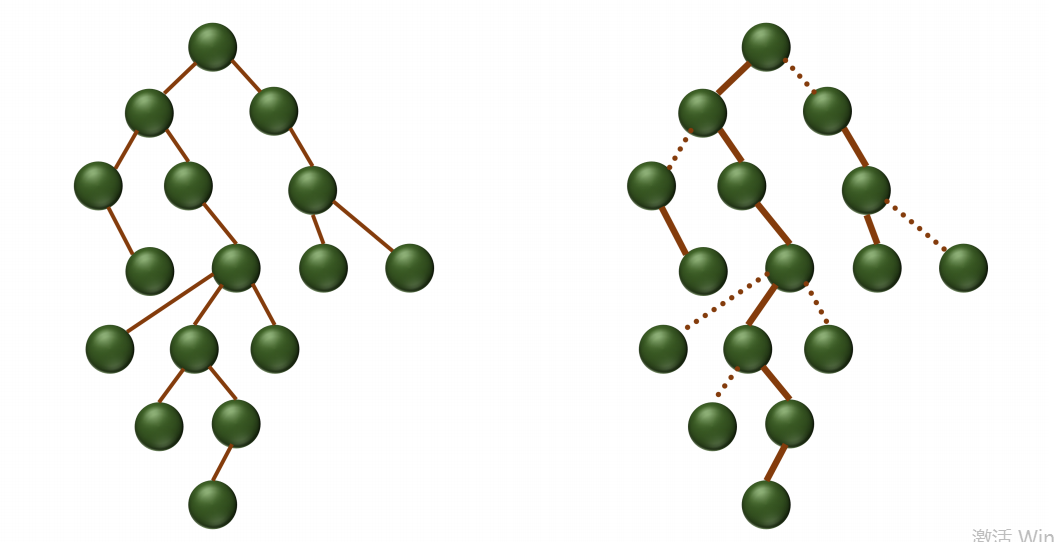
image-20200625194357565.png

我们看上面这张图，实线是重边，虚线是轻边

性质

用 \(size_i\) 表示以 \(i\) 为根的子树的大小

性质一：如果 \(v\) 是 \(u\) 的轻儿子，那么 \(size_v\leq\dfrac{size_u}{2}\)

反证法：如果 \(size_v>\dfrac{size_u}{2}\) 即轻儿子的大小超过了 \(size_u\) 的一半，那么 \(u\) 的其他儿子的子树大小一定小于 \(size_u\) 的一半，因此点 \(v\) 一定是重儿子，与假设不符。

性质二：任意点 \(u\) 到根的路径上轻边、重链条数都不大于 \(\log_2\!n\)。

证明：

考虑从根（\(size_{root}=n\)）开始往 \(u\) 走，每经过一条轻边，根据性质一，\(size\) 都至少会减小一半。

而走到 \(u\) 时 \(size_u\ge 1\)，因此经过的轻边条数必定 \(\leq \log_2\!n\)。

重链与重链之间是被轻边隔开的，因此经过的重链的条数与轻边的条数之差的绝对值不超过1。

性质三：一个点的子树内节点的 dfs 序是连续的

是不是一目了然了

模板题

我们先来接触一道模板题——洛谷P3384

【题目描述】

如题，已知一棵包含 \(N\) 个结点的树（连通且无环），每个节点上包含一个数值，需要支持以下操作：

操作 \(1\)： 格式： \(1\ x\ y\ z\) 表示将树从 \(x\) 到 \(y\) 结点最短路径上所有节点的值都加上 \(z\)。

操作 \(2\)： 格式： \(2\ x\ y\) 表示求树从 \(x\) 到 \(y\) 结点最短路径上所有节点的值之和。

操作 \(3\)： 格式： \(3\ x\ z\) 表示将以 \(x\) 为根节点的子树内所有节点值都加上 \(z\)。

操作 \(4\)： 格式： \(4\ x\) 表示求以 \(x\) 为根节点的子树内所有节点值之和

【输入格式】

第一行包含 \(4\) 个正整数 \(N,M,R,P\)，分别表示树的结点个数、操作个数、根节点序号和取模数（即所有的输出结果均对此取模）。

接下来一行包含 \(N\) 个非负整数，分别依次表示各个节点上初始的数值。

接下来 \(N-1\) 行每行包含两个整数 \(x,y\)，表示点 \(x\) 和点 \(y\) 之间连有一条边（保证无环且连通）。

接下来 \(M\) 行每行包含若干个正整数，每行表示一个操作，格式如下：

操作 \(1\)： \(1\ x\ y\ z\)；

操作 \(2\)： \(2\ x\ y\)；

操作 \(3\)： \(3\ x\ z\)；

操作 \(4\)： \(4\ x\)。

【输出格式】

输出包含若干行，分别依次表示每个操作 \(2\) 或操作 \(4\) 所得的结果（对 \(P\) 取模）

【样例输入】

5 5 2 24
7 3 7 8 0 
1 2
1 5
3 1
4 1
3 4 2
3 2 2
4 5
1 5 1 3
2 1 3

【样例输出】

2
21

【数据规模与约定】

对于 \(30\%\) 的数据： \(1 \leq N \leq 10,1 \leq M \leq 10\)；

对于 \(70\%\) 的数据： \(1 \leq N \leq {10}^3, 1 \leq M \leq {10}^3\)；

对于 \(100\%\) 的数据： \(1\le N \leq {10}^5, 1\le M \leq {10}^5,1\le R\le N,1\le P \le 2^{31}-1\)。

我们先考虑操作 \(3\) 和 \(4\)：

因为一个点的子树内节点的 dfs 序是连续的，我们就可以将一个点的 dfs 序看作它的位置

一个点的子树看作是一个 dfs 序的区间，子树加的操作相当于是在某个 dfs 序的区间内加上一个值，询问相当于是查询 dfs 序的某一个区间上的权值和。

问题转化为了区间加、区间查询和。

线段树可以在 \(O(m \log_2\!n)\) 的时间内完成。

再考虑操作 \(1\) 和 \(2\)：

我们可以用树链剖分来处理，在求 dfs 序时，我们按照优先重⼉⼦的顺序求出每个点的 dfs 序，此时⼀条重链上的节点的 dfs 序是连续的。

\(u\) 到 \(v\) 的路径可以拆分成两条只向上的链。

设 \(t=\operatorname{LCA}(u,v)\)，那么为 \(u\) 到 \(v\) 的路径上每个点权值 \(+x\) 相当于为 \(u\) 到 \(t\)、\(v\) 到 \(t\) 路径上的节点 \(+x\),而点 \(t\) 被
加了两次，减掉即可，查询的时候同理。

接下来我们只需要考虑一条自下而上的链 \((x, y)\)。 根据树链剖分的性质，这条路径是由不超过 \(\log_2\!n\) 条重链的一部分构成的。

当目前的 \(x\) 与 \(y\) 处在不同的重链中时，意味着 \(x\)需要跳过所在的重链，因此可以对这条重链从起点到 \(x\) 的 dfs 序区间进行操作，并跳到这条重链起点的父亲处。

当目前的 \(x\) 与 \(y\) 处在相同的重链中时，只需要将介于 \(y\) 与 \(x\) 之间的节点进行操作即可结束过程。

每次的操作都是一个线段树上的区间加、询问区间和的过程，单次 \(O(\log_2\!n)\)，而由于一次最多在 \(O(\log_2\! n)\)条重链上进行操作，因此总复杂度 \(O(m\log_2^2\!n)\)。

下面是代码讲解时间：

\(fa[i]\) 表示 \(i\) 的父亲节点，\(dep[i]\) 表示 \(i\) 的深度，\(son[i]\) 表示 \(i\) 的重儿子，\(Size[i]\) 表示 \(i\) 的子树大小；

\(id[i]\) 表示 \(i\) 的 dfs 序，也就是点 \(i\) 在线段树中的编号；\(bi[i]\) 表示 dfs 序为 \(i\) 的点的序号

\(top[i]\) 表示 \(i\) 所在重链的起点

首先，我们可以用一遍 dfs 求出 \(fa,Size,dep,son\) 数组，这个应该没什么好讲的

void dfs_first(int x,int _fa){
    Size[x]=1;
    for(rint i=head[x];i;i=nxt[i]){
        int y=ver[i];
        if(y==_fa) continue;
        fa[y]=x;
        dep[y]=dep[x]+1;
        dfs_first(y,x);
        Size[x]+=Size[y];
        if(Size[y]>Size[son[x]]) son[x]=y;
    }
}

当求出每个点的重儿子后，我们就可以再通过一次 dfs 来求出 \(id,top,bi\) 数组

void dfs_second(int x,int top_point){
    id[x]=++cnt; top[x]=top_point; bi[cnt]=x;
    if(!son[x]) return;//叶子节点直接退出
    dfs_second(son[x],top_point);//重儿子的链顶不变
    for(rint i=head[x];i;i=nxt[i]){
        int y=ver[i];
        if(y==fa[x]||y==son[x]) continue;
        dfs_second(y,y);//轻儿子是另一条重链的顶部
    }
}

考虑如何实现区间加法，类似于求 lca 的过程，在找 lca 的过程中将经过的区间统统 \(+v\)

void op_add(int x,int y,int v){
    while(top[x]!=top[y]){
        if(dep[top[x]]<dep[top[y]]) swap(x,y);
        change(1,1,n,id[top[x]],id[x],v);//将x到重链顶端这个区间+v
        x=fa[top[x]];
    }
    if(dep[x]<dep[y]) swap(x,y);
    change(1,1,n,id[y],id[x],v);
}

区间求和可以举一反三

然后美妙的线段树我就不解释了

整个的代码如下：

#include<bits/stdc++.h>
#define rint register int
using namespace std;
inline int read(){
    int s=0,f=1; char c=getchar();
    while(c<'0'||c>'9'){if(c=='-')f=0;c=getchar();}
    while(c>='0'&&c<='9') s=(s<<1)+(s<<3)+(c^48),c=getchar();
    return f?s:-s;
}
int n,m,root,Mod,val[100010];
int tot,head[100010],ver[200010],nxt[200010];
int Size[100010],son[100010],fa[100010],dep[100010];
int top[100010],id[100010],cnt,bi[100010];
void add(int x,int y){
    nxt[++tot]=head[x]; ver[tot]=y;
    head[x]=tot;
}
void dfs_first(int x,int _fa){
    Size[x]=1;
    for(rint i=head[x];i;i=nxt[i]){
        int y=ver[i];
        if(y==_fa) continue;
        fa[y]=x; dep[y]=dep[x]+1;
        dfs_first(y,x);
        Size[x]+=Size[y];
        if(Size[y]>Size[son[x]]) son[x]=y;
    }
}
void dfs_second(int x,int top_point){
    id[x]=++cnt; top[x]=top_point; bi[cnt]=x;
    if(!son[x]) return;
    dfs_second(son[x],top_point);
    for(rint i=head[x];i;i=nxt[i]){
        int y=ver[i];
        if(y==fa[x]||y==son[x]) continue;
        dfs_second(y,y);
    }
}
//下面是线段树板子
int Sum[400010],Add[400010];
void spread(int p,int l,int r){
    int mid=l+r>>1,lp=p<<1,rp=p<<1|1;
    if(Add[p]){
        Sum[lp]=1ll*(Sum[lp]+1ll*Add[p]*(mid-l+1)%Mod)%Mod;
        Sum[rp]=1ll*(Sum[rp]+1ll*Add[p]*(r-mid)%Mod)%Mod;
        Add[lp]=1ll*(Add[lp]+Add[p])%Mod;
        Add[rp]=1ll*(Add[rp]+Add[p])%Mod;
        Add[p]=0;
    }
    return;
}
void build(int p,int l,int r){
    if(l==r) return Sum[p]=val[bi[l]],void();
    int mid=l+r>>1,lp=p<<1,rp=p<<1|1;
    build(lp,l,mid); build(rp,mid+1,r);
    Sum[p]=Sum[lp]+Sum[rp];
}
void change(int p,int l,int r,int x,int y,int v){
    if(l>=x&&r<=y){
        Sum[p]=1ll*(Sum[p]+1ll*v*(r-l+1)%Mod)%Mod;
        Add[p]=1ll*(Add[p]+v)%Mod;
        return;
    }
    spread(p,l,r);
    int mid=l+r>>1,lp=p<<1,rp=p<<1|1;
    if(x<=mid) change(lp,l,mid,x,y,v);
    if(y>mid) change(rp,mid+1,r,x,y,v);
    Sum[p]=Sum[lp]+Sum[rp];
}
int ask_Sum(int p,int l,int r,int x,int y){
    if(l>=x&&r<=y) return Sum[p];
    spread(p,l,r);
    int mid=l+r>>1,lp=p<<1,rp=p<<1|1,val=0;
    if(x<=mid) val=1ll*(val+ask_Sum(lp,l,mid,x,y))%Mod;
    if(y>mid) val=1ll*(val+ask_Sum(rp,mid+1,r,x,y))%Mod;
    return val;
}
//上面是线段树板子
void op_add(int x,int y,int v){
    while(top[x]!=top[y]){
        if(dep[top[x]]<dep[top[y]]) swap(x,y);
        change(1,1,n,id[top[x]],id[x],v);
        x=fa[top[x]];
	}
    if(dep[x]<dep[y]) swap(x,y);
    change(1,1,n,id[y],id[x],v);
}
int op_sum(int x,int y){
    int ans=0;
    while(top[x]!=top[y]){
        if(dep[top[x]]<dep[top[y]]) swap(x,y);
        ans=1ll*(ans+ask_Sum(1,1,n,id[top[x]],id[x]))%Mod;
        x=fa[top[x]];
    }
    if(dep[x]<dep[y]) swap(x,y);
    ans=1ll*(ans+ask_Sum(1,1,n,id[y],id[x]))%Mod;
    return ans;
}
int main(){
    n=read(); m=read(); root=read(); Mod=read();
    for(rint i=1;i<=n;++i) val[i]=read();
    for(rint i=1;i<n;++i){
        int x=read(),y=read();
        add(x,y); add(y,x);
    }
    dfs_first(root,0); dfs_second(root,root); build(1,1,n);
    while(m--){
        int type=read();
        if(type==1){
            int x=read(),y=read(),z=read();
            op_add(x,y,z);
        }
        if(type==2){
            int x=read(),y=read();
            printf("%d\n",op_sum(x,y));
        }
        if(type==3){
            int x=read(),y=read();
            change(1,1,n,id[x],id[x]+Size[x]-1,y);
        }
        if(type==4){
            int x=read();
            printf("%d\n",ask_Sum(1,1,n,id[x],id[x]+Size[x]-1));
        }
    }
    return 0;
}

我就算打暴力，n 方修改，n方查询，也不会写树剖这种码量的模板题

真香~~

标签：入门,剖分,int,top,dfs,树链,leq,son,节点
来源： https://www.cnblogs.com/LCGUO/p/13192900.html

本站声明： 1. iCode9 技术分享网（下文简称本站）提供的所有内容，仅供技术学习、探讨和分享；
2. 关于本站的所有留言、评论、转载及引用，纯属内容发起人的个人观点，与本站观点和立场无关；
3. 关于本站的所有言论和文字，纯属内容发起人的个人观点，与本站观点和立场无关；
4. 本站文章均是网友提供，不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属；如您发现该文章侵犯了您的权益，可联系我们第一时间进行删除；
5. 本站为非盈利性的个人网站，所有内容不会用来进行牟利，也不会利用任何形式的广告来间接获益，纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。

关于我们 | 联系我们 | 留言反馈

专注分享技术，共同学习，共同进步。侵权联系[81616952@qq.com]

Copyright (C)ICode9.com, All Rights Reserved.

ICode9版权所有