标签:Group cdot 染色 Introduce circ 子群 陪集
目录- Introduce to Group
Introduce to Group
Definitions of Group
Group
Definition (Group)
若一个集合 \(G\) 和其上的运算 \(\circ\) 满足以下四个条件,则称二元组 \((G,\circ)\) 构成群,或称 \(G\) 在 \(\circ\) 下构成群。在不混淆的情况下,也可称 \(G\) 是群。
- 1. 封闭性:\(\forall f,g\in G\),\(f\circ g\in G\)。
- 2. 结合律:\(\forall f,g,h\in G\),\((f\circ g)\circ h=f\circ(g\circ h)\)。
- 3. 单位元存在性:\(\exists e\in G\),使得 \(\forall g\in G\),\(g\circ e=e\circ g=g\)。
- 4. 逆存在性:\(\forall f\in G,\exists g\in G\),使得 \(f\circ g=g\circ f=e\)。
其中 \(e\) 叫 单位元(幺元),对满足 \(f\circ g=g\circ f=e\) 的 \(g\),称为 \(f\) 的 逆元,记作 \(f^{-1}\)。\(f^{-1}\) 唯一。
Abelian Group (阿贝尔群)
Definition (Abelian Group)
当群 \(G\) 的运算满足 交换律 时,我们称 \(G\) 是一个 交换群 或 阿贝尔 (Abel) 群。
Special Groups
整数加法群
整数集合 \(\text{Z}\) 关于加法 \(+\) 构成群 \((\text{Z}, +)\)。
Cyclic Group (循环群)
对于任何正整数 \(m\),在模 \(m\) 的意义下的加法也构成群。
这个群非常重要,我们把它称为 \(m\) 阶 循环群 (Cyclic Group),记作 \(Z_m\)。
Symmetry Group (对称群)
所有 \(n!\) 个 \(n\) 元置换构成一个群,这个群被称为 \(n\) 元 对称群 (Symmetry Group),记作 \(S_n\)。
Alternating Group (交错群)
可以验证,所有 \(\lfloor \frac{n!}{2} \rfloor\) 个偶置换也构成一个群,这个群被称为 \(n\) 元 交错群 (Alternating group) ,记作 \(A_n\)。
Dihedral Group (二面体群)
对于一个正 \(n\) 边形,它的 旋转群 和 \(Z_n\) 是“本质相同”的(被称为“同构”),因此没必要去一个新的名称;
它的 旋转/翻转群 (意思就是把旋转和翻转构成的图形合起来的群) 共有 \(2n\) 个元素,
被称为 \(2n\) 阶 二面体群 (Dihedral Group),记作 \(D_{2n}\)。
Order (阶)
Definition (Order)
群 \(G\) 的元素个数称为 \(G\) 的 阶,简记为 \(|G|\)。
若群 \(G\) 有无穷多个元素,称 \(G\) 为 无限群;
否则称 \(G\) 为 有限群。
元和阶的概念不一样,不能乱用。
对于置换来说,元就是每个置换的元素个数,而不是置换群的元素(置换)个数。
- \((\text{Z},+)\) 为无限群。
- \(|Z_m|=m\)。
- \(|S_n|=n!\)。
- \(|A_n|=\lfloor \frac{n!}{2} \rfloor\)。
- \(|D_{2n}|=2n\)。
Subgroup (子群)
Subgroup
Definition (Subgroup)
设 \((G,\circ)\) 是群,若 \((G,\circ)\) 的子集 \((H,\circ)\) 对 同一种运算 \(\circ\) 也构成群,
则称 \((H,\circ)\) 是 \((G,\circ)\) 的子群,记作 \((H,\circ)\le (G,\circ)\)。
- \(A_n\le S_n\)。
- \(Z_n\le Z_m \iff n|m\)。
- \(Z_m \not\le (\text{Z},+)\),因为前者是模意义下的加法,后者是普通加法,两者不是同一种运算。
Generated Subgroup (生成子群)
Definition (Generated Subgroup)
设 \((G,\circ)\) 是群,\(S\) 为 \(G\) 的一个 非空子集,
则把包含 \(S\) 的所有子群的交称为 \(S\) 在 \(G\) 中生成的子群,记作 \(< S >\)。
Lagrange Theory (拉格朗日定理)
Coset (陪集)
Coset
Definition (Ceset)
对于群 \(G\) 和它的子群 \(H \le G\),对于一个元素 \(g \in G\),记集合 \(gH = \{g \circ h|h ∈ H\}\) 为 \(H\) 在 \(G\) 中导出的一个左陪集,同理可以定义右陪集。
- 在多数情况下,陪集不是子群。
Properties of Coset
我们只讨论右陪集,左陪集同理。
Property 1
Property 1
\(\forall g\in G\),\(|H|=|Hg|\)。
由于逆元唯一,对于 \(h_1,h_2\in H,h_1 \ne h_2\),有 \(h_1\circ g \ne h_2\circ g\)。
所以每一个 \(h\) 对应一个 \(hg\),这些 \(hg\) 互不相同,因此 \(|H|=|Hg|\)。
Property 2
Property 2
\(\forall g\in G\),\(g\in Hg\)。
由于 \(H\) 是个群,且与 \(G\) 是同一个运算,因此也包含幺元 \(e\),\(e\circ g=g\),因此 \(g\in Hg\)。
Property 3
Property 3
\(Hg=H \iff g\in H\)。
\(p\to q\):\(Hg\) 也是个群,\(g\) 与 \(H\) 内的元素进行运算得到群内元素,由群的封闭性,\(g\) 必须包含在群内。
\(q\to p\):仍然看作是 \(H\) 群内元素的运算,由封闭性可知。
Property 4
Property 4
\(Ha=Hb \iff a\circ b^{-1}\in G\)。
\(p\to q\):由 \(Ha=Hb\),有 \(Ha\circ b^{-1}=H\)。又由性质 3,\(a\circ b^{-1}\in G\)。(其实这种写法不太严谨...)
\(q\to p\):同由性质 3。反过来推就行了。
Property 5
Property 5
\(Ha \cap Hb \ne \emptyset \iff Ha=Hb\)。
这条性质很有用。
即对于 \(H\) 的任意两个左/右陪集,它们要么相等要么完全不相交。
设 \(c\in Ha\) 且 \(c\in Hb\),则 \(\exists h_1,h_2\in H\),使得 \(h_1\circ a=h_2\circ b=c\),
移项得 \(a\circ b^{-1}=h_2 \circ h_1^{-1} \in H\)。由性质 4,\(Ha=Hb\)。
那么其实可以打双箭头了。
Property 6
Property 6
\(H\) 的全体左/右陪集的并为 \(G\)。
由于 \(e\in H\),\(g\) 取遍 \(G\) 中的所有元素,显然。逃
Lagrange Theory
Lagrange Theory
\[|H| \times [G:H]=|G| \]
这里引入一个表述:
Definition
若 \(H\le G\),则 \([G:H]\) 表示 \(G\) 中 \(H\) 的不同陪集的数量。
\(H\) 的陪集大小均为 \(|H|\),它们要么不相交要么相等,全体陪集并为 \(G\),于是拉格朗日定理显然成立。
接下来在一般群的定义上,引入关于置换群的特殊概念。
Coloring (染色)
Coloring
Definition (Coloring)
一个 \(n\) 元染色,指的是对集合 \([n]\) 的每个元素分配一个物品(可以是颜色、数,等等) 的分配方案 。
比如,当 \(n=3\) 时, \(\{1 → 红, 2 → 绿, 3 → 粉\}\) 是一个染色,\(\{1 → 123, 2 → 254, 3 → 357\}\) 也是一个染色。
Action (作用)
置换群相对于其它的群有一个好处,它的元素是置换。而置换,是可以 作用 于染色的。
Definition (Action)
对于置换 \(f ∈ S_n\) 和染色 \(c ∈ C\),定义满足 \(f (i)\) 的颜色是 \(c[i]\) 的染色 \(c^{'}\),为 \(f\) 作用于 \(c\) 的结果,记为 \(f · c\),简记为 \(f c\)。即 \((f \cdot c) [i] = c[ f^{-1} (i)]\)。
可见,置换作用于染色后的结果仍是染色。
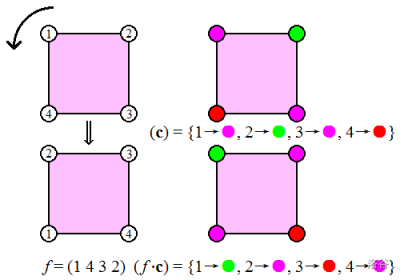
置换对染色满足以下两个 十分重要 性质:
- \(e \cdot c=c\)。
- \((f\circ g)\cdot c=f \cdot (g \cdot c)\)。
通过这两个性质可以得到抽象的染色概念:
Generalized Coloring
Definition (Generalized Coloring)
对于群 \(G\) (无须是置换群) 和一个全集 \(C\),对于 \(G\) 中任意一个元素和 \(C\) 中任意一个元素 \(c\),
定义运算 \(\cdot\) 满足 \(g · c ∈ C\),且满足如下两个性质:
- \(e \cdot c=c\)。
- \((f\circ g)\cdot c=f\cdot (g\cdot c)\)。
则称 \(C\) 是广义染色集合,\(C\) 中的元素 \(c\) 是广义染色。
\(C\) 是一个无穷集合。
Orbit-stabilizer Theorem (轨道-稳定子群定理)
Orbit (轨道)
Definition (Orbit)
考虑一个群 \(G\) 和一个染色 \(c\),将群中所有元素都对 \(c\) 作用,得到一个 \(C\) 的子集,记作 \(G\cdot c\)。
\[G\cdot c=\{g\cdot c |g\in G \} \]这个染色集合 \(G\cdot c\) 被称为 \(c\) 在 \(G\) 中的轨道。
- \(|G\cdot c| \le|G|\)。在染色集合 \(G\cdot c\) 中,一个染色可对应多个群中元素。
Definition (fixed)
对一个染色集合 \(X \subseteq C\),定义 \(G\cdot X=\{g\cdot c|g\in G,c\in X \}\)。
若 \(G\cdot X=X\),则称 \(X\) 在 \(G\) 下 固定 (fixed)。
可以理解为,给了 \(G\) 一个固定的运算,即使 \(X\) 要染成哪些颜色无法确定,每个 \(X\) 也都都是有限的。
不同的颜色可以导出不同的染色集合 \(X\),因此颜色导致 \(X\) 的个数无限。
Stabilizer Subgroup (稳定子群)
Definition (Stabilizer Subgroup)
对于一个置换群 \(G\) 和一个染色 \(c\),群中满足 \(g\cdot c=c\) 的置换 \(g\) 构成一个群,
称为染色 \(c\) 的 稳定子群,记作 \(G_c\)。
\(G_c\) 中的元素可称作 稳定子。
\(G_c\) 构成群,这一点可以由定义证明:
-
单位元存在性显然,\(e\cdot c=c\)。
-
逆元存在性:
考虑 \(g\cdot c=c \iff g^{-1}\cdot (g\cdot c)=g^{-1} \cdot c \iff (g^{-1}\circ g) \cdot c=g^{-1} \cdot c \iff g^{-1} \cdot c=c\)。
即若 \(g\) 在 \(G_c\) 内,\(g^{-1}\) 也在 \(G_c\) 内。
-
结合律:置换的合成显然满足。
-
封闭性:设有 \(f \cdot c=c,g\cdot c=c\),考虑代换:\(f\cdot(g\cdot c)=c \iff (f\circ g)\cdot c=c\)。
即 \(f \circ g\) 也在 \(G_c\) 内,满足封闭性。
Orbit-stabilizer Theorem
Orbit-stabilizer Theorem
对于置换群 \(G\) 和染色 \(c\),有:
\[|G\cdot c| \times |G_c|=|G| \]
-
Proof:
上文已证 \(G_c\) 是 \(G\) 的子群。
任取 \(G\) 中的元素 \(g\),对左陪集 \(gG_c=\{g\circ h|h\in G_c \}\) 中的元素 \(f=g\circ h_0\),
有 \(f\cdot c=(g\circ h_0)\cdot c=g\cdot(h_0\cdot c)=g\cdot c\),
因此 左陪集 \(gG_c\) 中的所有置换作用于 \(c\) 产生相同的一种染色 \(g\cdot c\)。
另一方面,对于两个不同的左陪集 \(g_1G_c,g_2G_c\),它们作用于 \(c\) 不能产生相同的染色。
补证:若它们能产生相同的染色,由上面的论述,只需把 \(g_1\cdot c\) 与 \(g_2\cdot c\) 拿出来考察,
由我们的假设,\(g_1\cdot c=g_2\cdot c \iff g_2^{-1}\cdot(g_1\cdot c)=c \iff (g_2^{-1}\circ g_1)\cdot c=c\)。
由稳定子群的定义,\(g_2^{-1}\circ g_1\in G_c\)。
由陪集性质 4,\(g_2^{-1}\circ g_1 \in G_c \iff g_1G_c=g_2G_c\),与假设矛盾,因此原命题成立。
总结一下前面两步,对于稳定子群 \(G_c\),先证明了同一陪集引出同一染色,以此为基础证明了不同陪集引出不同染色。
\(G_c\) 导出的不同陪集的数量为 \([G:G_c]\),而这也正是能导出的不同染色的数量。
\(G_c\) 作为 \(G\) 的一个子群,它的所有陪集的并为 \(G\),因此这些陪集能导出的染色集合就是 \(G\cdot c\),即 \([G:G_c]=|G\cdot c|\)。
由拉格朗日定理,\(|G|=|G_c|\times |G:G_c|=|G_c|\times |G\cdot c|\)。
轨道大小 \(\times\) 稳定子群大小 = 原群大小
标签:Group,cdot,染色,Introduce,circ,子群,陪集 来源: https://www.cnblogs.com/Schucking-Sattin/p/16544782.html
本站声明: 1. iCode9 技术分享网(下文简称本站)提供的所有内容,仅供技术学习、探讨和分享; 2. 关于本站的所有留言、评论、转载及引用,纯属内容发起人的个人观点,与本站观点和立场无关; 3. 关于本站的所有言论和文字,纯属内容发起人的个人观点,与本站观点和立场无关; 4. 本站文章均是网友提供,不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属;如您发现该文章侵犯了您的权益,可联系我们第一时间进行删除; 5. 本站为非盈利性的个人网站,所有内容不会用来进行牟利,也不会利用任何形式的广告来间接获益,纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。
