标签:筛法 int 质数 最小 三种 做法 primes 质因数
通常针对多个数
筛质数
给定一个正整数 $ n $,请你求出 $ 1 \sim n $ 中质数的个数。
输入格式
共一行,包含整数 $ n $。
输出格式
共一行,包含一个整数,表示 $ 1 \sim n $ 中质数的个数。
数据范围
$ 1 \le n \le 10^6 $
输入样例:
8
输出样例:
4
想法
三种筛法:
1. 朴素筛法
2. 埃氏筛法
3. 线性筛法
解法
1. 朴素筛法
时间复杂度:\(O(n\log n)\)
int p1(int n)
{
int cnt = 0;
for(int i = 2; i <= n; i++)
{
if(!st[i]) cnt ++;// 如果i是质数
for(int j = i; j <= n; j += i) // 此数所有的倍数都是合数,直接筛掉
st[j] = true;
}
return cnt;
}
2. 埃氏筛法
时间复杂度:\(O(n\log\log n)\)
此时间复杂度很低,如果\(n = 2^{32}\),\(O(\log n)\)的算法复杂度是\(32\),\(O(\log \log n)\)的算法复杂度是\(5\)
朴素筛法是不管你是不是合数是不是质数直接筛,但是那样会有许多重复的操作
事实上,合数不用去筛,因为合数该筛的数,它的因数已经在它前面筛完了
比如一个合数n,他的最小质因数为x,此时有一个数m是n的倍数,但是由于m是n的倍数,n是x的倍数,所以m也是x的倍数,因此,m肯定早已被x筛过了,那么n就无数可筛了
int p2(int n)
{
int cnt = 0;
for(int i = 2; i <= n; i++)
{
if(!st[i]) // 如果i是质数
{
cnt ++;
for(int j = i; j <= n; j += i) // 此数所有的倍数都是合数,直接筛掉
st[j] = true;
}
}
return cnt;
}
3. 线性筛法
时间复杂度:\(O(n)\)
用埃氏筛法筛数的时候会重复筛 —— 比如\(24\)既会被\(2\)筛又会被\(3\)筛,所以我们要找到筛掉合数的唯一方法,才能避免重复筛
首先整理思路,一个合数仅会被其最小质因数筛掉,这就是线性筛法中筛掉合数的唯一方法
先看代码:
int p3(int n)
{
for (int i = 2; i <= n; i ++ ) // 统计2-n质数的个数
{
if(!st[i]) primes[cnt++] = i; // 如果i是质数,那么就把i放进质数表里面
for(int j = 0; primes[j] <= n / i; j++) // 从小到大遍历质数表,筛掉合数,直到要筛的合数比n大
{
// 在这层循环里,每一次我们要筛掉的合数都是primes[j] * i
// i % primes[j] != 0的情况
// 此时primes[j]不是i的最小质因数,它小于i的最小质因数,原因见下文[1]
// 因此primes[j] * i的最小质因数就一定是primes[j],原因见下文[2]
st[primes[j] * i] = true; // 筛掉
if(i % primes[j] == 0) break;
// 当primes[j] 就是i的最小质因数时,应该用primes[j]筛完就break,因为后面的质数(primes[j+x])
// 肯定都大于i的最小质因数primes[j]
// 这个时候再用后面的质数筛(st[primes[j+x] * i] = true)的时候,
// 筛的合数肯定就不是用最小质因数筛的了,因为i已经有了最小质因数,
// 它可以拆解为最小质因数和另一个数的乘积,也就代表这个合数已经被前面的最小质因数筛过了
// 所以后面的质数对答案都没有贡献,不用考虑
}
}
return cnt;
}
[1]: 为什么 primes[j]不是i的最小质因数,它小于i的最小质因数?
A: 因为我们是从小到大枚举质数的,如果枚举到了i的最小质因数,它肯定会被
if(i % primes[j] == 0) break;break掉,而此时还没有break,也就是还没有枚举到i的最小质因数,因此primes[j]肯定小于i的最小质因数
[2]: 为什么primes[j] < i的最小质因数时,primes[j] * i的最小质因数就一定是primes[j]?
A: 因为\(primes[j] * i\)的最小质因数肯定是\(i\)的最小质因数或者是\(primes[j]\)的最小质因数中的较小者,\(primes[j]\)是个质数,质数的最小质因数就是它本身,再看i的最小质因数,由于\(primes[j] < i\),所以$primes[j]
- i\(的最小质因数就是\)primes[j]$
模拟:
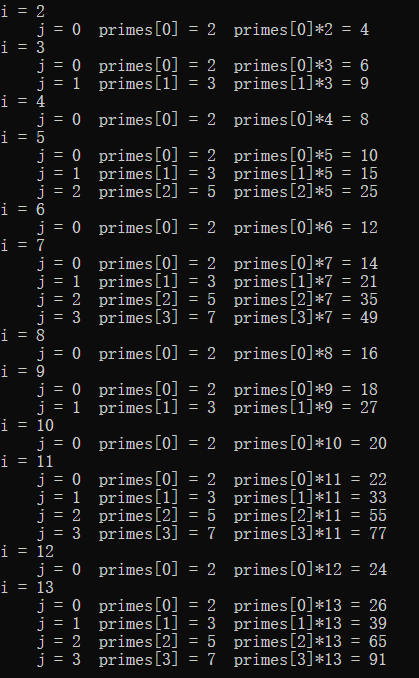
最后是三种筛法时间的对比

\(\Huge\color{Orchid}{点个赞吧!!}\)
标签:筛法,int,质数,最小,三种,做法,primes,质因数 来源: https://www.cnblogs.com/MoyouSayuki/p/16513617.html
本站声明: 1. iCode9 技术分享网(下文简称本站)提供的所有内容,仅供技术学习、探讨和分享; 2. 关于本站的所有留言、评论、转载及引用,纯属内容发起人的个人观点,与本站观点和立场无关; 3. 关于本站的所有言论和文字,纯属内容发起人的个人观点,与本站观点和立场无关; 4. 本站文章均是网友提供,不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属;如您发现该文章侵犯了您的权益,可联系我们第一时间进行删除; 5. 本站为非盈利性的个人网站,所有内容不会用来进行牟利,也不会利用任何形式的广告来间接获益,纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。
