使用树状数组优化\(LIS\)问题
一、与贪心+二分的方法对比
树状数组可以用来优化\(LIS\)问题,与贪心+二分的优化方式相比
优点:
-
二分作法只能计算出当前序列的\(LIS\),而树状数组可以计算出以每一个\(a(i)\)为结尾的\(LIS_i\)。(随进随查,不能算完一起来查)
-
学会了树状数组优化\(LIS\)后,后面有一道求最长上升序列和的问题,也可以使用树状数组优化为\(O(nlogn)\),而贪心+二分则无法优化那道题。
缺点:
- 同样是\(O(nlogn)\)的复杂度,树状数组的常数更大,贪心+二分的常数更小。可以通过\(AcWing 896\)的提交日志查看到结果对比,当然,你也可以说是此网站的数据问题,但有一定的代表性:
| 贪心+二分 | 树状数组(静态) | 树状数组(动态) |
|---|---|---|
| \(194\) \(ms\) | \(580\) \(ms\) | \(851\) \(ms\) |
- 贪心+二分的做法能计算出答案,想要获得具体方案则需要通过其它辅助办法记录路径。树状数组如果想要获得路径,也需要配合辅助数据进行计算(
这个我没实验过)。
二、树状数组是怎么优化问题的?
树状数组只是一个优化,本质上还是原始的\(O(n^2)\)动态规划求\(LIS\),解决的是在递推时计算\(f[i]\)时,优化了
for(int j=1;j<i;j++)
if(a[i]>a[j]) f[i]=max(f[i],f[j]+1)
因为这就是一个暴力的枚举过程,所以造成了\(O(n^2)\)的时间复杂度,现在想要找一个办法,将此处的寻找能接、可接的\(f[i]\)进行优化。
问题描述
- 我\(a[i]\)前面的
- 值比我小的:\(a[j]<a[i]\)
- 最大那个
- 我要接在它的后面 \(f[j]+1\)
解决办法
-
我\(a[i]\)前面的
for(i=0;i<n;i++)保证每个\(a[i]\)讨论时,都只关心它前面的计算结果。
-
值比我小的:\(a[j]<a[i]\)
- 这个需要转化一下:复制数组进行排序+离散化,可以知道当前要处理的数字\(a[i]\)的排名,我只关心排名比我小的信息。
-
最大的那个
- 采用的是用树状数组维护从开头到排名的最大值。 树状数组本质上是一个数据结构:
-
对外提供:快速查询到目前为止,排名\(k\)位的\(LIS[k]=query(k)\)。
注意:动态录入+动态获取!
随着更多数据的录入,查询结果会变化,不能最终一并查询,只能是边录边查! -
内部实现:以二进制形式分块保存的统计数据,以本题而言,就是分块保存的范围内最大值,此最大值,并不能直接使用,对外提供查询功能时,需要枚举所有前序分块,汇总最大值。
-
- 采用的是用树状数组维护从开头到排名的最大值。 树状数组本质上是一个数据结构:
举个栗子:
7
3 1 2 1 8 5 6
通过排序加去重,给每个数字都标识了它在原序列中排名是多少:
排序+去重数组\(b[]\)
| 下标 | \(0\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) |
|---|---|---|---|---|---|---|
| 排名 | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) |
| 数值 | \(1\) | \(2\) | \(3\) | \(5\) | \(6\) | \(8\) |
整出来个\(b[]\)数组有啥用呢?就是为了知道当前要操作的数字\(a[i]\)它的排名是多少,根据它的排名,可以知道它的前一名,查询到前一名时的最大\(LIS\)值,我接在它后面\(+1\)就是答案。
配合下面的树状数组结构图以便深入理解:
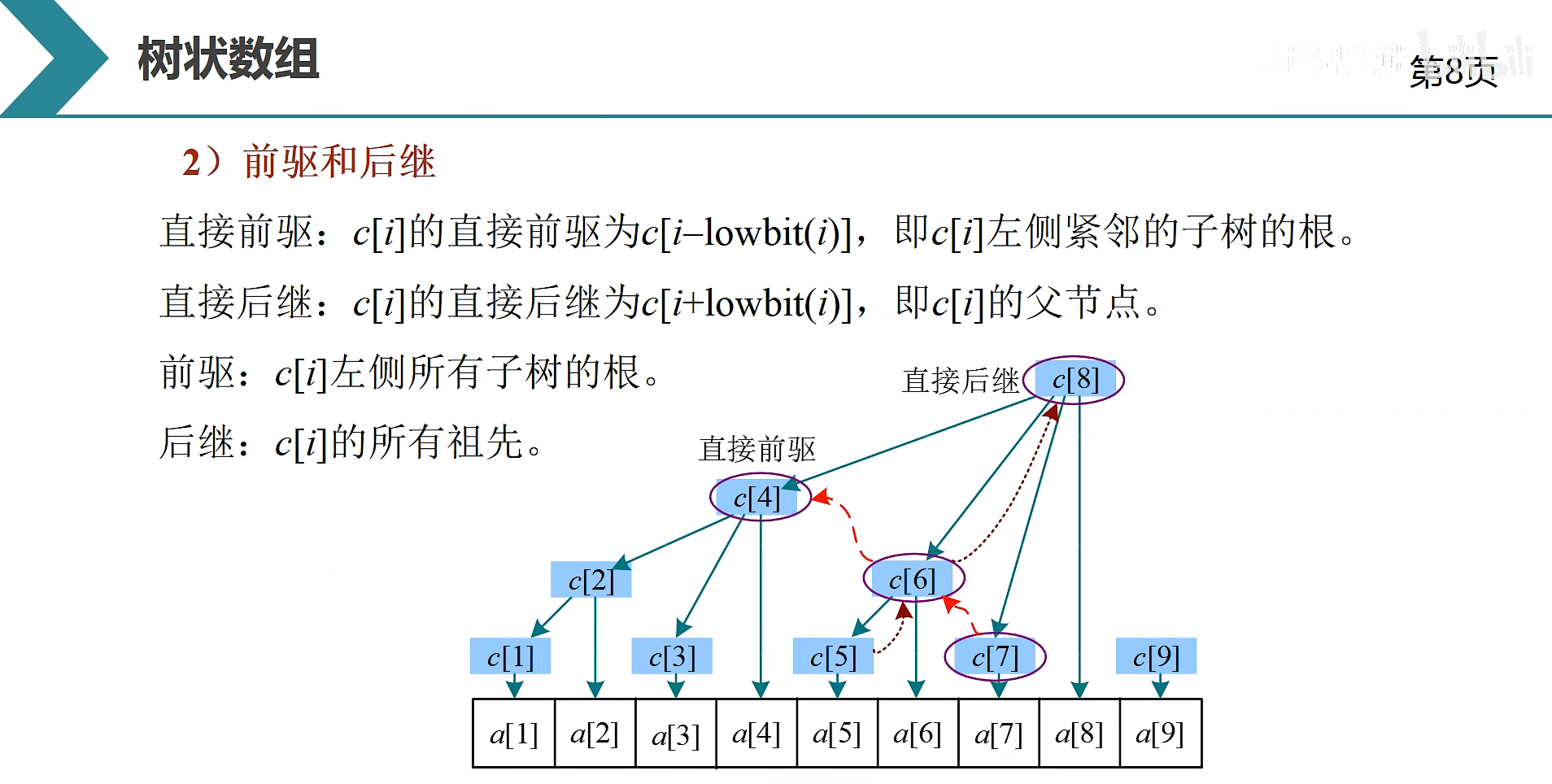
编写一个带调试信息的代码,输出调试信息,方便理解
\[talk is cheap,show me your code! \]#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x & -x)
const int N = 1e5 + 10;
int n, a[N];
int b[N], bl; //离散化数组,用于辅助树状数组
int c[N]; //树状数组
int res; //结果
//计算x值在原序列中的排名
int get(int x) {
return lower_bound(b, b + bl, x) - b + 1;
}
//单点更新x
void update(int i, int x) {
for (; i <= bl; i += lowbit(i)) c[i] = max(c[i], x);
}
//求1~i的最大值
int query(int i) {
int s = 0;
for (; i; i -= lowbit(i)) s = max(s, c[i]);
return s;
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i++) scanf("%d", &a[i]), b[i] = a[i];
//离散化,用于获取 x值->排名k 的关系
sort(b, b + n);
// bl:去重后的长度
bl = unique(b, b + n) - b;
/*
测试用例:
7
3 1 2 1 8 5 6
*/
for (int i = 0; i < n; i++) {
puts("==============================================");
printf("i:%d a[i]=%d\n", i, a[i]);
int k = get(a[i]); // a[i]的排名k
printf("rank:%d rank-1:%d\n", k, k - 1);
int t = query(k - 1) + 1;
printf("LIS[rank-1]:%d ", t - 1);
printf("LIS[rank]:%d\n", t);
res = max(res, t);
update(k, t); //第k大的数,会接在第k-1大的数后面,才会获取到更大的连续LIS值
puts("FenWickTree:");
for (int i = 1; i <= bl; i++) printf("%d ", c[i]);
puts("");
}
return 0;
}
输出的结果:
==============================================
i:0 a[i]=3
rank:3 rank-1:2
LIS[rank-1]:0 LIS[rank]:1
FenWickTree:
0 0 1 1 0 0
==============================================
i:1 a[i]=1
rank:1 rank-1:0
LIS[rank-1]:0 LIS[rank]:1
FenWickTree:
1 1 1 1 0 0
==============================================
i:2 a[i]=2
rank:2 rank-1:1
LIS[rank-1]:1 LIS[rank]:2
FenWickTree:
1 2 1 2 0 0
==============================================
i:3 a[i]=1
rank:1 rank-1:0
LIS[rank-1]:0 LIS[rank]:1
FenWickTree:
1 2 1 2 0 0
==============================================
i:4 a[i]=8
rank:6 rank-1:5
LIS[rank-1]:2 LIS[rank]:3
FenWickTree:
1 2 1 2 0 3
==============================================
i:5 a[i]=5
rank:4 rank-1:3
LIS[rank-1]:2 LIS[rank]:3
FenWickTree:
1 2 1 3 0 3
==============================================
i:6 a[i]=6
rank:5 rank-1:4
LIS[rank-1]:3 LIS[rank]:4
FenWickTree:
1 2 1 3 4 4
==============================================
理解一下代码的执行流程
i:0 a[i]=3
rank:3 rank-1:2
LIS[rank-1]:0 LIS[rank]:1
FenWickTree:
0 0 1 1 0 0
\(3\)开始,查询到排名是\(3\),查询前一个排名的\(LIS[2]=query(2)\),第一个嘛,前面没有,所以是\(0\),把它的排名在前序排名上面加\(1\),记\(c[3]=1\),含义为本片片长\(c[3]\)知道自己管辖范围内(\(a[3]\))的最长上升子序列长度为\(1\)。同时,向各级领导汇报,告诉\(c[4]\),你的孩子\(c[3]\)目前\(LIS\)是\(1\),你们看看用不用更新一下自己的最大值。如果此时要查询排名\(3\)以下的最长上升子序列长度值,就是执行\(query(3)\),代码会去找\(c[3]\)和\(c[2]\),\(pk\)大小后返回较大值。
i:1 a[i]=1
rank:1 rank-1:0
LIS[rank-1]:0 LIS[rank]:1
FenWickTree:
1 1 1 1 0 0
\(1\)开始,查询到排名是\(1\),查询前一个排名的\(LIS[0]=query(0)=0\),标识\(c[1]=1\),同时也要向上尝试\(PK\)更新\(c[2],c[4]\),结果\(c[2]\)被修改为\(1\)。
i:2 a[i]=2
rank:2 rank-1:1
LIS[rank-1]:1 LIS[rank]:2
FenWickTree:
1 2 1 2 0 0
\(2\)开始,查询到排名是\(2\),查询前一个排名的\(LIS[1]=query(1)\),知道前面最大值是\(1\),则\(c[2]=2\),同时更新\(c[4]=2\)
i:3 a[i]=1
rank:1 rank-1:0
LIS[rank-1]:0 LIS[rank]:1
FenWickTree:
1 2 1 2 0 0
\(1\)开始,查询到排名是\(1\),查询前一个排名的\(LIS[0]=query(0)=0\),将\(c[1]\)尝试修改为\(1\),并尝试更新\(c[2],c[4]\),当然,现在更新不了,人家原来的就比\(1\)大。
i:4 a[i]=8
rank:6 rank-1:5
LIS[rank-1]:2 LIS[rank]:3
FenWickTree:
1 2 1 2 0 3
\(8\)开始,查询到排名是\(6\),查询前一个排名的\(LIS[5]=query(5)\),此时\(c[5]=0\),则\(max(c[5],c[4])=2\),表示现在排名前\(5\)位之前的\(LIS=2\),所以\(c[6]=2+1=3\)。
i:5 a[i]=5
rank:4 rank-1:3
LIS[rank-1]:2 LIS[rank]:3
FenWickTree:
1 2 1 3 0 3
\(5\)开始,查询到排名是\(4\),查询前一个排名的\(LIS[3]=query(3)=max(c[3],c[2])=2\),则\(c[4]=2+1=3\)
i:6 a[i]=6
rank:5 rank-1:4
LIS[rank-1]:3 LIS[rank]:4
FenWickTree:
1 2 1 3 4 4
\(6\)开始,查询到排名是\(5\),查询前一个排名的\(LIS[4]=query(4)==c[4]=3\),则\(c[5]=3+1=4\)
三、树状数组实现代码1
//运行时间: 601 ms
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x & -x)
const int N = 1e5 + 10;
int n, a[N];
int b[N], bl; //离散化数组,用于辅助树状数组
int tr[N]; //树状数组
int res; //结果
//计算x值在原序列中的排名
int get(int x) {
return lower_bound(b, b + bl, x) - b + 1;
}
//单点更新x
void update(int i, int x) {
for (; i <= bl; i += lowbit(i)) tr[i] = max(tr[i], x);
}
//求tr[1]~tr[i]的最大值
int query(int i) {
int s = 0;
for (; i; i -= lowbit(i)) s = max(s, tr[i]);
return s;
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i++) scanf("%d", &a[i]), b[i] = a[i];
//离散化,用于获取 x值->排名k 的关系
sort(b, b + n);
// bl:去重后的长度
bl = unique(b, b + n) - b;
for (int i = 0; i < n; i++) {
int k = get(a[i]); //值a[i]的排名k
int t = query(k - 1) + 1;
res = max(res, t);
update(k, t); //第k大的数,会接在第k-1大的数后面,才会获取到更大的连续LIS值
}
//输出
printf("%d\n", res);
return 0;
}
四、树状数组实现代码2
//运行时间: 582 ms
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x & -x)
const int N = 1e5 + 10;
int n, a[N];
int b[N], bl; //离散化数组,用于辅助树状数组
int tr[N]; //树状数组
int res; //结果
//计算x值在原序列中的排名
int get(int x) {
return lower_bound(b, b + bl, x) - b + 1;
}
//单点更新x
void update(int i, int x) {
for (; i <= bl; i += lowbit(i)) tr[i] = max(tr[i], x);
}
//求tr[1]~tr[i]的最大值
int query(int i) {
int s = 0;
for (; i; i -= lowbit(i)) s = max(s, tr[i]);
return s;
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i++) scanf("%d", &a[i]), b[i] = a[i];
//离散化,用于获取 x值->排名k 的关系
sort(b, b + n);
// bl:去重后的长度
bl = unique(b, b + n) - b;
for (int i = 0; i < n; i++) {
int k = get(a[i]); //值a[i]的排名k
int t = query(k - 1) + 1;
update(k, t); //第k大的数,会接在第k-1大的数后面,才会获取到更大的连续LIS值
}
//输出
printf("%d\n", query(bl));
return 0;
}
五、树状数组实现代码3
//运行时间: 863 ms
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x & -x)
const int N = 1e5 + 10;
int n, a[N];
//树状数组
int tr[N];
//离散化数组,提供指定值对应的排名,辅助树状数组
vector<int> b;
int res; //结果
//计算x值在原序列中的排名
int get(int x) {
return lower_bound(b.begin(), b.end(), x) - b.begin() + 1;
}
//求tr[1]~tr[i]的最大值
int query(int i) {
int s = 0;
for (; i; i -= lowbit(i)) s = max(s, tr[i]);
return s;
}
//单点更新x
void update(int i, int x) {
for (; i <= n; i += lowbit(i)) tr[i] = max(tr[i], x); //注意这里是跳着取max,不是传统的sum求和
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
b.push_back(a[i]);
}
//离散化,用于存储a数组按值由小到大去重排序的结果,这样就可以使用二分查找 值->排名
sort(b.begin(), b.end());
b.erase(unique(b.begin(), b.end()), b.end());
for (int i = 1; i <= n; i++) { //按原输入序进行遍历,这样才符合LIS的要求
int k = get(a[i]); //获取值a[i]的整体大小排名k
int t = query(k - 1) + 1; //在树状数组中查找排名为k-1的最大数量,再加1才是当前连接上后的数量
update(k, t); //将排名k更新目前最优解t
}
//输出
printf("%d\n", query(b.size()));
return 0;
}
六、总结与感悟
- 树状数组用于快速查询\(O(logN)\)前缀和,区间和,区间\([1\sim i]\)的最大值。
- 树状数组强调的是 一边修改一边查询的场景,纯静态的、离线查询的,不如原始前缀和。
- 树状数组中保存的数据,是具有片断性的, 不能直接拿来用,要现用现组装。(不要和我犟说\(c[4],c[8]\)就不用组装之类的话~)
- 树状数组能做的事:单点修改,可使用减法原则的区间查询,对于区间修改请移步线段树。
- 相对线段树,代码量少。
标签:树状,int,rank,数组,LIS,排名 来源: https://www.cnblogs.com/littlehb/p/16465901.html
本站声明: 1. iCode9 技术分享网(下文简称本站)提供的所有内容,仅供技术学习、探讨和分享; 2. 关于本站的所有留言、评论、转载及引用,纯属内容发起人的个人观点,与本站观点和立场无关; 3. 关于本站的所有言论和文字,纯属内容发起人的个人观点,与本站观点和立场无关; 4. 本站文章均是网友提供,不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属;如您发现该文章侵犯了您的权益,可联系我们第一时间进行删除; 5. 本站为非盈利性的个人网站,所有内容不会用来进行牟利,也不会利用任何形式的广告来间接获益,纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。
