标签:mu Dirichlet 前缀 limits sum times a1 应用
\[\Huge\text{Dirichlet 前缀和及其应用} \]全文概要
- Dirichlet 前缀和定义;
- Dirichlet 前缀和的算法,及其拓展;
- Mobius 函数,Mobius 反演以及它们与 Dirichlet 前缀和,Dirichlet 卷积之间关系;
- 具体应用。
1 Dirichlet 前缀和定义
给定数列 \(a_i\),定义数列 \(b_i=\sum\limits_{d|i} a_d\),即所有下标为该下标约数的原数组之和。
例子:\(n=10,a_i=\left\{1,4,6,9,2,4,5,6,4,3\right\}\),则 \(b_i=\left\{1,5,7,14,3,15,6,20,11,10\right\}\)
2 模板问题与复杂度
2.1 Dirichlet 前缀和
2.1.1 算法说明
\(n\le 2\times 10^7\),说明要用优于/微劣于 \(\mathcal{O}(n)\) 的算法。
对于一个数 \(a_j\),它会被计算到 \(b_{1\times j},b_{2\times j}\dots\) 中。
而对于 \(a_k(k\ge 1,k|j)\) ,可以发现会被记入 \(b_{1\times k},b_{2\times k},b_{3\times k}\dots\)
可见 \(b_{1\times j},b_{2\times j}\dots\) 也肯定会被包含;
因此可以得到一个结论:\(b_j\) 会被 \(b_{1\times j},b_{2\times j},b_{3\times j}\dots\) 所包含。
但是如果直接计算 \(b_{4\times j}\),会被 \(b_{j}\) 和 \(b_{2\times j}\) 同时计入,有重复;
于是稍稍变换计算方式:每次乘以一个不超过其下标本身的质数,就可以解决这个问题,也能够保证不重复地计算。
核心代码:
for(int i=1;i<=cnt;i++)
for(int j=1;j*pr[i]<=n;j++) a[j*pr[i]]+=a[j];
其中 cnt 是所有素数的总数,pr[i] 为第 \(i\) 个素数。
2.1.2 算法正确性证明
下面证明上述代码是正确的,也即不重复且不遗漏:
下证第 \(i(i\le cnt)\) 轮过后,对于满足 \(l|d,\frac{d}{l}=pr_1^{\alpha_1}pr_2^{\alpha_2}\dots pr_i^{\alpha_i}\) 的 \(l\),令这些 \(l\) 组成集合 \(S_{i,d}\)。\(b_d=\sum\limits_{l\in S_{i,d}} a_l\)
\(i=0\) 时,显然成立!(\(b_i=a_i\))
假设对 \(i=k-1\) 成立,此时 \(b_1=a_1\),\(j=1\) 成立!
假设 \(b_1\dots b_p\) 均满足如上结论,
\(p=j+1\) 时,如果 \(pr_i|j+1\),那么 \(b_{j+1}\leftarrow b_{j+1}+b_{\frac{j+1}{pr_i}}\),即 \(b_{j+1}=\sum\limits_{l\in{S_{k-1,j+1}}}a_l+\sum\limits_{l\in{S_{k,\frac{j+1}{pr_i}}}}a_l\)
由定义可知 \(S_{k,\frac{j+1}{pr_i}}\cap S_{k-1,j+1}=\varnothing\),且 \(S_{k,\frac{j+1}{pr_i}}\cup S_{k-1,j+1}=S_{k,j+1}\);
所以 \(b_{j+1}=\sum\limits_{l\in{S_{k,j+1}}}a_l\)
得证!
2.1.3 举例验证
举个例子直观地验证一下各个数字的变化情况:\(n=10,cnt=4,pr_i=\left\{2,3,5,7\right\}\)
初始情况:
a1,a2,a3,a4,a5,a6,a7,a8,a9,a10
\(i=1,pr_i=2\) 后:
a1,a2+a1,a3,a4+a2+a1,a5,a6+a3,a7,a8+a4+a2+a1,a9,a10+a5
\(i=2,pr_i=3\) 后:
a1,a2+a1,a3+a1,a4+a2+a1,a5,a6+a3+a2+a1,a7,a8+a4+a2+a1,a9+a3+a1,a10+a5
\(i=3,pr_i=5\) 后:
a1,a2+a1,a3+a1,a4+a2+a1,a5+a1,a6+a3+a2+a1,a7,a8+a4+a2+a1,a9+a3+a1,a10+a5+a2+a1
\(i=4,pr_i=7\) 后:
a1,a2+a1,a3+a1,a4+a2+a1,a5+a1,a6+a3+a2+a1,a7+a1,a8+a4+a2+a1,a9+a3+a1,a10+a5+a2+a1
2.2 Dirichlet 后缀和
类似的,给定数列 \(a_i\),定义数列 \(b_i=\sum\limits_{i|d} a_d\)。
即所有下标为该下标倍数的原数组之和。
我们可以如下操作:每次同样乘以一个不超过其下标本身的质数,但是由于前缀变为后缀,因此把计算顺序改变一下——变成从后向前计算。
为什么呢?画张图。
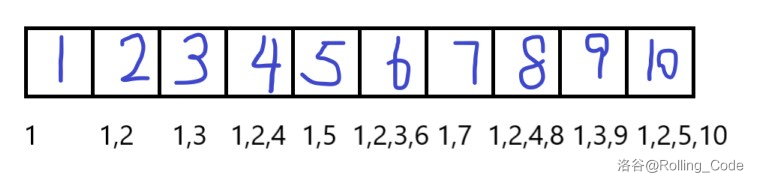
上图为 Dirichlet 前缀和,下面的数字代表给他贡献的 \(a\) 数组下标,上面是 \(b\) 数组下标
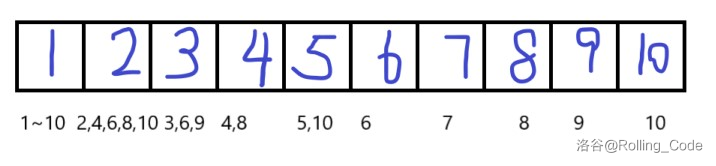
上图为 Dirichlet 后缀和
核心代码:
for(int i=1;i<=cnt;i++)
for(int j=n/pr[i];j>=1;j--) a[j]+=a[j*pr[i]];
用类似 Dirichlet 前缀和的证法也可以得证!
2.3 逆推 Dirichlet 前缀和
即已知前缀和 \(b_i\),求原数组 \(a_i\);
相当于是一个差分(Dirichlet 差分)。
所以直接按照前缀和的代码倒序遍历即可。
核心代码:
for(int i=cnt;i>=1;i--)
for(int j=n/pr[i];j>=1;j--) a[j*pr[i]]-=a[j];
2.4 逆推 Dirichlet 后缀和
即已知前缀和 \(b_i\),求原数组 \(a_i\);
还是 Dirichlet 差分,可以按照后缀和代码倒序遍历。
核心代码:
for(int i=cnt;i>=1;i--)
for(int j=1;j*pr[i]<=n;j++) a[j]-=a[j*pr[i]];
2.5 Dirichlet 前缀和及其拓展复杂度
这个算法复杂度为 \(\mathcal{O}(\sum\limits_{\text{质数p}\le n} \dfrac{n}{p})\),与埃氏筛的复杂度相同,因此可以得知复杂度约为 \(\mathcal{O}(n\log\log n)\)
3 Dirichlet 卷积 和 Mobius 反演
3.1 Dirichlet 卷积 和 Mobius 函数之间的关系
3.1.1 什么是Dirichlet 卷积
Dirichlet 卷积,是定义在两个数论函数 \(f,g\) 上的 \(f*g\) 满足 \((f*g)(n)=\sum\limits_{d|n}f(d)\times g(n/d)\)
Dirichlet 卷积满足如下的规律:
-
交换律:\(f*g=g*f\)
-
结合律:\((f*g)*h=f*(g*h)\)
-
分配律:\(f*(g+h)=f*g+f*h\)
-
存在单位元:定义 \(\epsilon(n)=[n=1]\),则 \(f*\epsilon =f\)
-
保持积性:如果 \(f,g\) 都是积性函数,那么 \(f*g\) 也是积性函数。
3.1.2 什么是 Mobius 函数
Mobius 函数用 \(\mu\) 来表示。
如果 \(n=1\) 则 \(\mu(n)=1\);
如果 \(n\) 没有平方因子,则 \(\mu(n)=(-1)^{\text{n的素因子个数}}\);
如果 \(n\) 有平方因子,则 \(\mu(n)=0\)。
定理一:
\[\epsilon(n)=\sum\limits_{d|n}\mu(d) \]即 \(\epsilon=\mu*1\);
证明:
设 \(n=p_1^{\alpha_1}p_2^{\alpha_2}\dots p_k^{\alpha_k},n'=\prod\limits_{i=1}^{k} p_i\)
所以 \(\sum\limits_{d|n} \mu(d)=\sum\limits_{d|n'}\mu(d)=\sum\limits_{i=0}^{k}C^i_k\times (-1)^k=(1+(-1))^k=[n=1]=\epsilon(n)\)
得证!
所以我们可以利用 Dirichlet 卷积处理 Mobius 函数!
3.1.3 莫比乌斯反演
如果函数 \(f,g\) 满足
\[f(n)=\sum\limits_{d|n} g(d) \]则
\[g(n)=\sum\limits_{d|n}\mu(d)f(\dfrac{n}{d}) \]证明:根据定义可以得到 \(f=g*1\)
两边同时卷上 \(\mu\)
可以得到:
\[f*\mu=g*1*\mu \]\[\because 1*\mu =\epsilon \]\[\therefore f* \mu=g*\epsilon=g \]因为 \(\mu(p^k)=[k=1]\),而且 \(\mu\) 是积性函数,所以可以用线性筛模板计算。
void prime(ll n){
mu[1]=1;
for(int i=2;i<=n;i++){
if(!vst[i]) pr[++cnt]=i,mu[i]=-1;
for(ll j=1;j<=cnt&&i*pr[j]<=n;j++){
vst[i*pr[j]]=1;
if(!(i%pr[j])){mu[i*pr[j]]=0;break;}
mu[i*pr[j]]=-mu[i];
}
}
}
3.2 复杂度的分析
假设我们现在要算 \(f=g*1\),如果对于每一个 \(f_i\) 都是暴力计算,复杂度是 \(\mathcal{O}(\sqrt n)\) 的,总和是 \(\mathcal{O}(n\sqrt n)\);
如果预计算完了每个数的约数列表,可以得知复杂度约为 \(\mathcal{O}(n/1+n/2+\dots n/n)\),而每个数计算也需要其约数个数的复杂度。
而 \(\lim\limits_{n\rightarrow \infty}\sum\limits_{i=1}^{n}\dfrac{n}{i}=n\ln n\)(素数定理)
所以预计算约数的复杂度总和是 \(\mathcal{O}(n\log n)\)。
而我们使用了 Dirichlet 卷积以后复杂度下降为 \(\mathcal{O}(n\log \log n)\)。
主要的差距就在于 Dirichlet 卷积以后我们省去了重新计算 \(f_d(d|i)\) 的过程。
举个例子:在前两种情况,计算 \(f_{10}\) 时,前两种方法都会将 \(f_5\) 重新计算,但是事实上在 Dirichlet 卷积当中 之前计算好的 \(f_5\) 可以被重复利用,进而减少计算次数。
3.3 从多维空间看 Dirichlet 前缀和
我们回过头来看一看 \(n=10\) 时最后的 \(b_i\):
a1,a2+a1,a3+a1,a4+a2+a1,a5+a1,a6+a3+a2+a1,a7+a1,a8+a4+a2+a1,a9+a3+a1,a10+a5+a2+a1
乍看之下似乎没有规律。
如果我们将 \(i\) 质因数分解以后,并且以各个质因数的幂次作为坐标呢?

举个比较形象的例子:(为了表示方便暂时只列出前三根轴)红色线条框出的立方体即为 \(b_{30}\) 所包含的所有 \(a_d\) 在这个空间中的坐标,而蓝色框出的部分即为 \(b_{100}\) 所包含的 \(a_d\)。
如果我们要在这个空间内做差分的话,由容斥原理,令 \(n=p_1^{\alpha_1}p_2^{\alpha_2}\dots p_k^{\alpha_k}\) 可得
\[a_{n}=\sum\limits_{d|n,\frac{n}{d}=p_1^{\beta_1}p_2^{\beta_2}\dots p_k^{\beta_k},\beta_i\in{0,1}} (-1)^{\sum\limits_{i=1}^{n} \beta_i}\times b_d \]\[\therefore a_{n}=\sum\limits_{d|n,\frac{n}{d}=p_1^{\beta_1}p_2^{\beta_2}\dots p_k^{\beta_k},\beta_i\in{0,1}} \mu\left(\dfrac{n}{d}\right)\times b_d \]由 Mobius 函数的定义,如果存在平方的质数为 \(n\) 约数,\(\mu(n)=0\)。
\[\therefore a_{n}=\sum\limits_{d|n} \mu\left(\dfrac{n}{d}\right)\times b_d \]\[\therefore a_{n}=\sum\limits_{d|n} \mu\left(d\right)\times b_{\frac{n}{d}} \]这就是 Dirichlet 差分!
再看一下 Mobius 反演的式子:
\[g(n)=\sum\limits_{d|n}\mu(d)f(\dfrac{n}{d}) \]会发现 Dirichlet 差分和 Mobius 反演本质一样。
借此发现了 Dirichlet 前缀和/差分 与 Mobius 反演之间的关系。
4 具体的应用
即求
\[\sum\limits^{n}_{x=1}\sum\limits^{m}_{y=1}[\gcd(x,y)\text{为质数}] \]设 \(g(x)\) 为 \(\gcd(i,j)=x\) 的个数,\(f(x)\) 为 \(\gcd(i,j)=k\times d,k=1,2,\dots\) 的个数。(假设是单组数据)
\[\therefore g(x)=\sum\limits^{n}_{i=1}\sum\limits^{m}_{j=1}[\gcd(i,j)=d],f(x)=\sum\limits^{n}_{i=1}\sum\limits^{m}_{j=1}[\gcd(i,j)=kd] \]\[f(x)=\sum\limits_{d|x} g(d)=\left\lfloor\dfrac{n}{x}\right\rfloor\left\lfloor\dfrac{m}{x}\right\rfloor \]\[g(x)=\sum\limits_{x|d}\mu\left(\left\lfloor\dfrac{d}{x}\right\rfloor\right)f(x) \]即求
\[\sum\limits_{\text{p是质数}}\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{m} [\gcd(i,j)=p] \]把 \(g(p)\) 的表达式代入。
\[\sum\limits_{\text{p是质数}}g(p) \]可以使用莫比乌斯反演!
\[\sum_{\text{p是质数}}\sum\limits_{p|d}\mu\left(\left\lfloor\dfrac{d}{p}\right\rfloor\right)f(d) \]改变枚举项,枚举
\[\left\lfloor\dfrac{d}{p}\right\rfloor \]\[\sum\limits_{\text{p是质数}}\sum\limits_{d=1}^{\min(\frac{n}{p},\frac{m}{p})}\mu(d)f(d\times p)=\sum\limits_{\text{p是质数}}\sum\limits_{d=1}^{\min(\frac{n}{p},\frac{m}{p})}\mu(d)\left\lfloor\dfrac{n}{d\times p}\right\rfloor\left\lfloor\dfrac{m}{d\times p}\right\rfloor \]把 \(
d\times p\) 换元成
\(T\) 可以得到:
再交换一下 \(\sum\) 的顺序:
\[\sum\limits_{T=1}^{\min(n,m)}\left\lfloor\dfrac{n}{T}\right\rfloor\left\lfloor\dfrac{m}{T}\right\rfloor\sum\limits_\text{p|T,p是质数}\mu\left(\left\lfloor\dfrac{T}{p}\right\rfloor\right) \]所以就可以线性筛 \(\mu\) 函数,整除分块并记录前缀和。
复杂度 \(\mathcal{O}(n+\sqrt{n})\)。
4.后记
通过 Dirichlet 前缀和,构建起了 Mobius 函数,Mobius 反演,及高维前缀和的关系。
但是 Dirichlet 前缀和不仅在计算机中有所应用,数学中也可以见到他的身影。
比如在证明与 \(\varphi\) 等数论函数相关的式子里,可以派上用场。
标签:mu,Dirichlet,前缀,limits,sum,times,a1,应用 来源: https://www.cnblogs.com/RollingCode/p/Dirichlet.html
本站声明: 1. iCode9 技术分享网(下文简称本站)提供的所有内容,仅供技术学习、探讨和分享; 2. 关于本站的所有留言、评论、转载及引用,纯属内容发起人的个人观点,与本站观点和立场无关; 3. 关于本站的所有言论和文字,纯属内容发起人的个人观点,与本站观点和立场无关; 4. 本站文章均是网友提供,不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属;如您发现该文章侵犯了您的权益,可联系我们第一时间进行删除; 5. 本站为非盈利性的个人网站,所有内容不会用来进行牟利,也不会利用任何形式的广告来间接获益,纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。
