前言:
记得去年五一的时候我买了lxl的那个数据结构的五一专题。
结果当时死活听不懂……
现在回头来看看,真的学着挺轻松的。
所以写个简单的总结吧。
树状数组(Binary Index Tree)
现在真的觉得这个东西神奇的一批。
也不知道是哪个天才想到这种数据结构。
居然可以用 \(\log n\) 个元素来查询前缀和。
真的很牛逼啊。
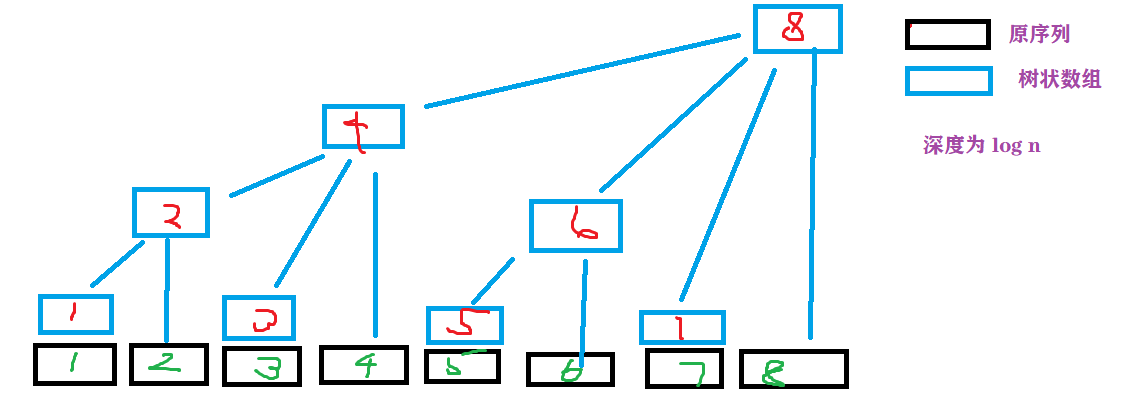
树状数组真的玄乎,所以直接上原理图吧。
这就是一个树状数组。
我们设 \(a[]\) 为原序列,\(t[]\) 为树状数组。
那么这样的构造有什么用呢?
看一下 \(t[]\) 的特点:
\[t_1=a_1 \]\[t_2=a_1+a_2 \]\[t_3=a_3 \]\[t_4=a_1+a_2+a_3+a_4 \]\[t_5=a_5 \]\[t_6=a_5+a_6 \]\[t_7=a_7 \]\[t_8=a_1+a_2+a_3+a_4+a_5+a_6+a_7+a_8 \]发现了么?树状数组里下标和 \(2\) 有关系的似乎表示的长度要长的多?
那么这就牵扯到树状数组的基本原理了。
正如所有的整数都可以表示成2的幂和,我们也可以把一串序列表示成一系列子序列的和。
采用这个想法,我们可将一个前缀和划分成多个子序列的和
而划分的方法与数的2的幂和具有极其相似的方式。
一方面,子序列的个数是其二进制表示中1的个数,
另一方面,子序列代表的t[i]的个数也是2的幂。
——Peter M. Fenwick,1994
看不懂?没事,我们先看看它能干些什么。
单点修改操作
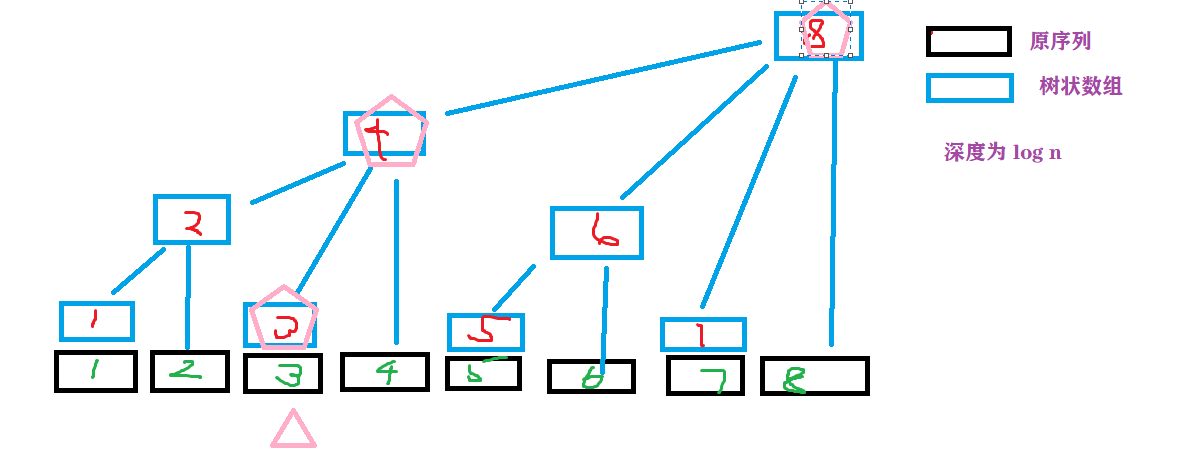
如果我们修改 \(a[3]\) 的值。
考虑会影响到哪些 \(t[i]\)
看一下我最开始列的那一个表。
会发现这只会影响 \(t_3,t_4,t_8\)
那我们修改这些 \(t[i]\) 就好。
你会发现,这里我们所用的数的个数是小于等于 \(\log(n)\)的
也就是说它可以在 \(\log (n)\) 的时间内完成单点修改。
前缀和
前面你也可以看到。
\[t_8=a_1+a_2+a_3+a_4+a_5+a_6+a_7+a_8 \]所以树状数组能否维护前缀和?
可以的。
看上面的图。
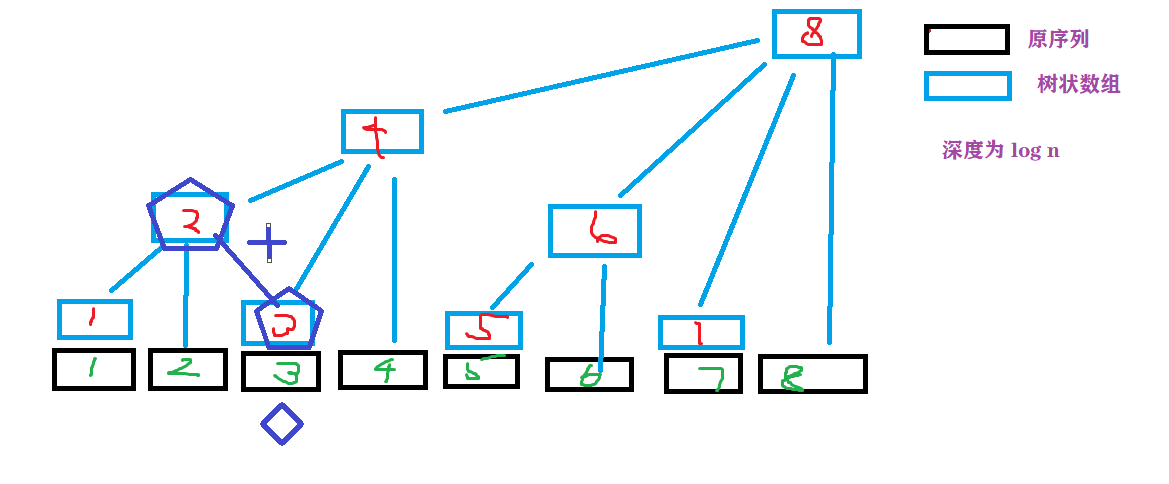
我们如果要查询 \(a[1,3]\) 的前缀和。
只需要用 \(t_2+t_3\) 就可以了。
这里我们查询的时候用的数的个数也是小于等于 \(\log (n)\)的。
所以结合上文。
我们可以发现。
树状数组是一个利用 \(\log(n)\) 以内个的元素去凑出子序列的信息,以此来维护序列的数据结构。
当然,如果你要区间查询和,用一下 \(sum(r)-sum(l-1)\) 不就好了?
这时候有人就要问了:怎么去确定要用那些元素来维护呢?
这时候就要请出 lowbit 先生了~
它可以返回一个数二进制表示下的最低位。
也就是返回二进制数的最后一位1,并且在返回时附带其后面的0
那么这个性质可以干啥?因为树状数组的本身性质。
我们可以直接用 for(初值;条件;i+(-)=lowbit(i)) 来找出要用的元素。
真妙啊~。
那么代码如下:
int lowbit(int x){
return x&-x;
}
void modify(int x,int y){
for(register int i=x;i<=n;i+=lowbit(i)){
t[i]+=y;
}
}
int sum(int x){
int res=0;
for(register int i=x;i;i-=lowbit(i)){
res+=t[i];
}return res;
}
int query(int l,int r){
return sum(r)-sum(l-1);
}
其实 sum 操作的时候就是在不断的去掉 i 末尾的 1 并把它变成 0
而 modify 则是一点一点加上去(其实就是和 sum 互逆的过程)。
区间修改:
这个也比较容易。
我们知道差分珂以 \(\text{O}(1)\) 修改区间。
所以我们直接用树状数组维护一个差分数组就好了。
区间加区间和:
这个是在上一个的基础上推出来的。
我们知道,我们维护在树状数组上维护的那个差分数组 \(t[]\)
它的前缀和 \(\sum^x_{i=1}t[i]\) 就是 \(a[x]\) 的增加的值。
所以也就是说:原序列\(a\)中前缀和\(sum[1,x]\)的总增加量就是:
\[\sum^x_{i=1}\sum^i_{j=1} t[j] \]上式又等于:
\[\sum^x_{i=1}(x-i+1)\times t[i] \]\[=(x+1)\sum^x_{i=1}t[i]-\sum^x_{i=1}i\times t[i] \]看一下最终的这个柿子。
也就是说,我们如果要维护原序列中前缀和的“增量”
我们只需要在树状数组上维护两个差分数组。一个维护 \(t[i]\) ,一个维护 \(i\times t[i]\) 然后就可以维护了。
至于前缀和怎么维护?
很简单。
我们知道树状数组是一个能维护动态前缀和的数据结构。
而我们这里把动态的“增量” 单独提出来维护。
所以我们可以直接在读入原数组的时候维护一下原始的前缀和。
然后询问动态前缀和的时候就直接用前缀和加上增量就可以了。
区间询问同理。
维护异或前缀和的树状数组
这题是一个典型例子。
当然lg上有四道和它基本一样的重题,可以自行到讨论区寻找。
这道题要你维护一个01序列。支持查询某个数的值。还有对于 \([l,r]\) 中的0,1,让0变成1,1变成0。
很简单。
看到01序列我们第一时间就应该想到 异或。
因为 \(0/1 \operatorname{xor} 1\) 就是给这个数取反。
根据异或本身具有的运算性质。
我们可以直接给异或维护前缀和。
所以这道题直接维护异或的区间加和单点查就好。
code:
void modify(int x){
for(register int i=x;i<=n;i+=lowbit(i)){
t[i]^=1;
}
}
int sum(int x){
int res=0;
for(register int i=x;i;i-=lowbit(i)){
res^=t[i];
}return res;
}
//-------
//in function main():
read(n),read(q);
while(q--){
int op,l,r;read(op);
if(op==1){read(l),read(r),modify(l),modify(r+1);}
else{read(l),write(sum(l))ent;}
}
统计数在区间中的出现次数的树状数组
设 $t[i] $表示 \(i\) 在集合 \(A\) 中出现的次数。
那么 \(\sum^r_{i=l}t[i]\) 就是范围 \([l,r]\) 中 有多少个数。同理用树状数组维护即可。
(上面的那题的4道重题就要用这个)
例题:
因为这个东西的原理并不会拿出来考什么的(也没啥可以考的)
而且其实它能做的,线段树都能做(只是BIT常数小可以用来优化某些题)。
所以就写的比较粗糙(。
标签:前缀,树状,sum,笔记,算法,数组,序列,维护 来源: https://www.cnblogs.com/BTeqwq/p/binary-index-tree.html
本站声明: 1. iCode9 技术分享网(下文简称本站)提供的所有内容,仅供技术学习、探讨和分享; 2. 关于本站的所有留言、评论、转载及引用,纯属内容发起人的个人观点,与本站观点和立场无关; 3. 关于本站的所有言论和文字,纯属内容发起人的个人观点,与本站观点和立场无关; 4. 本站文章均是网友提供,不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属;如您发现该文章侵犯了您的权益,可联系我们第一时间进行删除; 5. 本站为非盈利性的个人网站,所有内容不会用来进行牟利,也不会利用任何形式的广告来间接获益,纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。