首页 > 其他分享> 文章详细

NOI 一轮复习 I：二分图网络流

2021-04-29 17:36:07 阅读：327 来源： 互联网

标签：二分匹配最大增广路径最小复习 NOI

NOI 一轮复习 I：二分图网络流

阅读须知：

本系列博客主要为个人复习所用，可供各位参考。

整理的知识点不会涉及较为偏僻的知识点，以 NOI 考察过的知识点为主。

按照目前的想法，想分成 数据结构、分治、数论函数、线性代数、连通性、二分图网络流、计算几何、字符串、组合计数、杂论、论文选做 这些板块进行整理，由于只是最初设想，想必此后会有更新。

知识清单/目录：

二分图概念与判定
二分图最大匹配
二分图最大权匹配
Hall 定理
网络最大流
最小费用最大流
上下界网络流
网络流扩展与建模举例

注意事项：

其实本文的一大重点是证明各种二分图和网络流算法的理论基础，模板并不会详解，建模也只是一个部分。
限于作者水平，本文一般不讨论网络流算法的时间复杂度，在分析例题复杂度时将其视为一个整体模块。
本文所讨论的图（特别是当边无权时）一般为简单图，且一般认为 $O(|E|)\ge O(|V|)$。

因为网络流 24 题比较老旧，就不想写了。

将在 1~2 周内随缘更新。

1. 二分图概念与判定

定义：对于无向图 $G=(V,E)$，若存在将 $V$ 划分成两个不相交子集 $A,B$ 的方案，使得 $A,B$ 的点导出子图都不含边，则称 $G$ 为二分图，$A,B$ 为 $G$ 的两部。

这即是说，$(u,v)\in E\rightarrow (u\in A,v\in B)\lor (u\in B,v\in A)$。

由此，我们也可以用二染色来定义二分图：二分图是可以被二染色的图。

这里存在一个小性质：若二分图 $G=(V,E)$ 包含 $C$ 个连通分量，则其二染色的方案为 $2^C$，这是因为每个连通分量恰有两种染色方法。

下面给出二分图的一个性质和判定定理：

定理：图 $G=(V,E)$ 为二分图，当且仅当 $G$ 中不存在长度为奇数的圈。

证明：

若 $G$ 中存在长度为奇数的圈，设环上点依次为 $v_1,\ldots,v_{2n-1}$，使得 $v_i$ 与 $v_{i+1}$ 为邻居（$v_{2n}=v_1$），考虑这个环的二染色情况，易知 $v_1,v_3,\ldots,v_{2n-1}$ 同色，则 $v_1$ 和 $v_{2n-1}$ 是一对相邻的同色点，不符合二染色的定义，故必要性得证。

当 $G$ 中不存在长度为奇数的圈时，考虑每一个连通分量，以任意点为根求出一棵生成树，由于不存在奇环，所以任一条非树边连接的两个顶点深度不同奇偶，考虑将所有深度为奇数的点染为黑色，深度为偶数的点染为白色，这就得到了一种二染色方案，故充分性得证。

推论：二分图 $G=(V,E)$ 的任意子图为二分图。

推论：无向图 $G=(V,E)$ 是二分图当且仅当其每个连通分量都是二分图。

根据上面的定理和证明过程，我们可以得到判定给定无向图是否是二分图的算法：

设给定的图为 $G=(V,E)$，由第二条推论，只需分别判定 $G$ 的每个连通分量是否是二分图。
对于 $G$ 中的一个连通分量，对其进行 DFS，求出一棵搜索树并记录每个点的深度，遇到返祖边时，判定这条边两端点的深度是否同奇偶，如果同奇偶则 $G$ 不是二分图，若对于所有返祖边都有两端点深度不同奇偶，则 $G$ 是二分图。
在实现时，只需要记录每个点深度的奇偶性，事实上这等价于模拟对 $G$ 进行二染色的过程。
时间复杂度为 $O(|E|)$。

事实上，结合上面的过程还可以得到一些比较显然的小结论：例如连通图 $G$ 不是二分图当且仅当对于任意生成树 $T$ 都存在恰好包含一条非树边的奇环，这些结论应该更贴近连通性方面的知识了。

二分图有关路径长度的浅显性质：二分图中任意两点间路径经过的边数奇偶性确定，反之，一个连通非二分图中任意两点间路径经过的边数奇偶性都不确定。

例题 $1$：[Luogu P1330] 封锁阳光大学

给定无向图 $G=(V,E)$，求最小的点集 $A\subseteq V$ 使得 $\forall (u,v)\in E$ 有 $u\in A$ 或 $v\in A$ 恰好成立其一，或报告无解。

容易发现，若存在这样的 $A$，则 $G$ 是以 $A$ 和 $V\backslash A$ 构成两部的二分图，因此若 $G$ 不是二分图则无解。

当 $G$ 是二分图时，考虑到每个连通分量的独立性，对每个连通分量分别考虑，将其二染色后取点数较少的一边加入 $A$ 中，点数较多的一边加入 $V\backslash A$ 中即可。

时间复杂度为 $O(|E|)$。

例题 $2$：[NOIP 2010] 关押罪犯

有 $N$ 个罪犯和两座监狱，罪犯间有 $M$ 对形如 $(u,v,w)$ 的关系表示 $u,v$ 两名罪犯若在同一监狱则会发生影响力为 $w$ 的冲突事件，求合理分配每个罪犯到某一座监狱后，发生的最大影响力的冲突事件的影响力最小值。

二分答案 $W$，考虑所有影响力关系 $(u,v,w)$，建立 $V=\{1,2,\ldots,N\},\ E=\{(u,v,w)|w> W\}$ 的无向图 $G$，则所有冲突事件影响力都能不大于 $W$ 当且仅当 $G$ 是二分图，判定之。

时间复杂度为 $O(M\log (\max w))$。

例题 $3$：[HNOI 2019] 校园旅行

给定无向图 $G=(V,E)$，每个点有 $0$ 或 $1$ 的一个标记，有 $q$ 组询问，每组询问给定 $s,t\in V$，你需要求出是否存在一条 $s\to t$ 的路径 $P$，使得路径经过的点的标记拼成一个回文串。

$O(|V|^2+q)$。

考虑一个由标记全为 $0$ 或标记全为 $1$ 的点构成的大小不小于 $2$ 的连通分量，若 $P$ 经过了这个连通分量，则我们可以在 $P$ 中任意增添 $2n$ 个这种标记（只需选择一条边来回经过一下），因此对于这些大小不小于 $2$ 的连通分量，我们只关心 $P$ 经过这个连通分量时在路径中增加的 $0$ 段或 $1$ 段的长度奇偶性。

当这个连通分量 $C$ 不是二分图时，从一个点到另一个点经过点数的奇偶性是确定的；反之当 $C$ 不是二分图时经过点数的奇偶性是可变的，因此我们可以缩去这个连通块内的一些边，只需要满足它是否是二分图这一性质不变即可。

如果它是二分图，显然只需要保留一棵生成树即可，否则只需要保留一棵生成树的基础上任意增加一个奇环，例如增加一条自环。

（甚至不必是生成树，任意一个连通二分图均可）

同样的道理，当我们把这样一个连通块视为一个整体时，连接不同连通块的边也可以通过相似的方法缩成只剩一个生成树或加上一条自环。

（这一部分只能是生成树，不能是任意一个连通二分图）

可以论证，大小为 $1$ 的连通分量的存在不会对上述过程的正确性产生影响，因为与之对应的在路径中的对称点也必然只有一个，并不影响（但请注意，这要求我们在缩两侧不同标记的边时保留的是原图 $G$ 中的生成树，而不是把所有之前的连通块缩成一点后再求生成树）。

此时 $O(|E|)=O(|V|)$，我们考虑一个 $|E|^2$ 的 BFS 算法，以 $s\to s$ 这样的路径和 $s\to t$ 且 $s,t$ 是相邻的同标记点这样的路径为起点不断向两侧扩展即可。

时间复杂度为 $O(|V|^2+q)$。

2. 二分图最大匹配

二分图最大匹配问题，即对于给定的二分图 $G=(V,E)$，求出大小最大的边集 $A\subseteq E$ 使得 $A$ 中不存在两条共端点的边。

我们下面将介绍求解二分图最大匹配的匈牙利算法。

令 $P$ 是一个匹配，其中的边称为匹配边，匹配边的端点称为匹配点，如果一条路径从一个未匹配的左部点出发到达一个未匹配的右部点，交替经过不在 $P$ 中的边和在 $P$ 中的边，则称该路径为一条增广路。

匈牙利算法依赖一个重要结论：$P$ 是二分图的最大匹配，当且仅当图中不存在增广路。

必要性容易证明：若存在增广路，则将增广路上全体非匹配边改为匹配边，匹配边改成非匹配边，就得到了一组更大的匹配。

充分性证明：若 $P$ 不是最大匹配，设最大匹配为 $P'$，显然存在左部点 $x$ 不在 $P$ 中而在 $P'$ 中，假设在 $P'$ 中它匹配了 $y$，若 $y$ 在 $P$ 中是非匹配点，那么我们已经找到了一条增广路 $x\to y$，否则对 $y$ 在 $P$ 中匹配的点重复上述过程，则我们或者得到一条增广路，或者得到了一个增广路删去一条边的结构，将其中所有边取反，可以将 $P'$ 调整为一个和 $P$ 更为“接近”的最大匹配，不断执行此过程，若一直未找到增广路，最后 $P'=P$，说明 $P$ 是最大匹配，矛盾。

upd 一个更严谨的充分性证明：考虑一个最大匹配 $P'$，求出 $P,P'$ 的对称差 $T=P\Delta P'$（是一个边导出子图），由于 $P,P'$ 是匹配，所以 $T$ 中所有点度数不大于$2$，因此 $T$ 是由若干环和若干链组成的，如果 $P$ 比 $P'$ 小，那么对称差中属于 $P'$ 的部分就要更多，而对于环和偶链来说二者所占边数相等，所以必定有一个奇链，即增广路。

上面充分性的证明已经部分蕴含了匈牙利算法的内容：

枚举 $i=1,\ldots,n$，其中 $n$ 为左部点数量，时刻维护左部点当前前缀 $1,\ldots,i-1$ 与全体右部点的一组最大匹配 $P$，考虑将 $i$ 加入：
以 $i$ 为端点进行 DFS 寻找增广路，假设寻找以左部点 $x$ 开始的增广路，首先枚举 $x$ 的邻居 $y$，若 $y$ 是非匹配点或者从 $y$ 匹配的点出发存在增广路，那么我们就找到了一条以 $x$ 开始的增广路（对于前者，$x\to y$，对于后者，$x\to y\to z\to \ldots $）；
如果找到了一条增广路，答案增加 $1$；
为了控制算法复杂度，在对于每个 $i$ 寻找增广路时，如果从一个 $x$ 出发时寻找失败，下次就可以直接返回，如果从一个 $y$ 的匹配点出发时寻找失败，下次也不必再检查 $y$。

匈牙利算法基于贪心原则：一旦一个点进入匹配，就不会重新成为非匹配点，因此当找不到增广路时表示 $i$ 在保持 $1,\ldots,i-1$ 的匹配情况不变时一定无法加入最大匹配中。

由此，我们可以知道：若将匹配的左部点记为 $1$，未匹配的左部点记为 $0$，则按照枚举顺序拼接左部点的匹配情况，匈牙利算法求出的最大匹配是字典序最大的。

简单说说二分图匹配和匈牙利算法的一种组合理解：

考虑从拟阵交的角度刻画二分图最大匹配问题，令 $S=E$，$2^S$ 的子集 $I_1$ 为满足导出子图中所有左部点度数不超过 $1$ 的边集，$I_2$ 为满足导出子图中所有右部点度数不超过 $1$ 的边集，下面证明 $M_1=(S,I_1)$ 和 $M_2=(S,I_2)$ 为拟阵：

以 $M_1$ 为例，这里直接采用定义的方法证明：

显然，$\varnothing\in I_1$；
遗传性：显然若 $A\in I_1$，则对于 $B\subseteq A$ 有 $B\in I_1$；
交换性：若 $A,B\in I_1$，$|A|<|B|$，任取 $B$ 到处子图中一个度数为 $1$ 而在 $A$ 导出子图中度数为 $0$ 的点，将其对应的边加入 $A$ 中，仍然在 $I_1$ 中。

那么匹配就是 $M_1$ 和 $M_2$ 的交了，要求最大匹配，即 $M_1$ 与 $M_2$ 的拟阵交问题。

回想拟阵交中的扩展过程，我们维护当前最大交 $A$，每次选择一条路径 $v_1\to \ldots\to v_m$，使得 $(A\backslash \{v_{2i}\})\cup v_{2i+1}\in I_1$ 且 $(A\backslash \{v_{2i}\})\cup v_{2i-1}\in I_2$，其实这就是匈牙利算法中寻找的增广路的边集。

例题 $4$：[NOI 2009] 变换序列

给定数列 $A_{1\ldots n}$，求字典序最小的排列 $P_{1\ldots n}$ 使得 $|P_i-i|=A_i$。

考虑建立二分图，左右部各有 $n$ 个点，左边的点 $i$ 向右边的点 $i+A_i$ 和 $i-A_i$ 连边，则一种完美匹配对应了一种合法的 $P$。

为了使得 $P$ 的字典序最小，我们倒序枚举左部点，并在寻找增广路时优先找右部编号较小的点，这是因为寻找增广路的过程中右部点的匹配点不断更改，按这个顺序进行枚举总可以使得当前点匹配的是编号最小的点。

二分图最大匹配还可以用来解决一些其他模型。

二分图最小点覆盖

最小点覆盖问题指的是在给定图中选择尽量少的点，使得每条边至少有一个点被选。

我们考虑将二分图最大匹配写成线性规划形式，每条边视作变量，每个点视作限制：

\[\max \sum\limits_{i=1}^m x_i \]

\[s.t. \begin{cases}\sum\limits_{i=1}^mw(j,i)x_i\leq 1 \\ x_i\ge 0\end{cases}\]

其中 $w(j,i)$ 表示 $j$ 是否是边 $i$ 的一个端点。

我们可以证明：上面问题中的代价矩阵是一个全幺模矩阵，因此其最优解等于整数规划解，即 $x_i\in \{0,1\}$，这说明了我们用线性规划描述二分图匹配的合理性。

（因为证明过程比较复杂，这里不写了，需要注意的是，若是一般图匹配则此处矩阵不是全幺模矩阵。）

将其对偶：

\[\min\sum\limits_{j=1}^n y_j \]

\[s.t. \begin{cases} \sum\limits_{j=1}^n w(j,i)y_j\ge 1 \\ y_j\ge 0 \end{cases}\]

也就是说每条边的两个端点中至少要选一个，这也就是最小点覆盖问题了。

根据强对偶定理，我们可以得到：

定理：二分图最小点覆盖大小等于最大匹配大小。

随后，我们给出一种最小点覆盖的构造方法：

在求完最大匹配后，从二分图的每个左部未匹配点出发进行一次寻找增广路，然后将途径的所有点设为已经过标记。
取左侧所有未标记点和右部所有标记点，它们构成一组点覆盖。
下面证明这是一组点覆盖：如果存在一条边两端都没有选，说明其左侧是标记点，右侧是非标记点，但是在那个左侧点被标记后，右侧的点随后就会被经过，所以这是不可能的。
下面证明这组点覆盖的大小等于最大匹配大小：对于每条匹配边，或者左侧右侧同时被标记，或者同时没被标记，因此必定恰有一个点被选；而对于一条非匹配边，假设左侧点不是匹配点，那么必然被标记，假设右侧点不是匹配点，那么必然不被标记（否则找到了一条增广路），因此只有所有匹配边的恰好一边在这组点覆盖中。

实际上，我们还容易证明任何一组点覆盖大小 $\ge$ 任何一组匹配大小，根据上面的构造，也可以得到定理。

二分图最大独立集

最大独立集问题指的是在给定图中选择尽量多的点，使得其导出子图不含边。

对于任何一张无向图，我们有如下定理成立：

定理：最大独立集大小与最小点覆盖大小之和等于点数。

这是因为任何一组独立集取补后就得到一组点覆盖，独立集与点覆盖是一一对应的。

所以在二分图中我们就有：

定理：二分图最大独立集大小与最大匹配大小之和等于点数。

例题 $5$：

求在 $n\times m$ 棋盘上最多放置多少个不会互相攻击的骑士。

对于格子 $(i,j)$，如果 $2|i+j$ 则作为左部点，否则作为右部点，在每一对可以互相攻击的格子间连边，此二分图的最大独立集即为答案。

值得注意的是，许多类似的棋盘问题都可以用黑白染色的方法转化成二分图相关的问题。

与本题类似还有 Luogu P5030 之类，注意每题的染色方法可能不同。

二分图最小边覆盖

最小边覆盖的定义类似最小点覆盖，即用最少的边覆盖所有的点。

如果不存在孤立点，则二分图最小边覆盖等于最大独立集大小，即总点数减去最大匹配大小。

首先，最大独立集中任何两个点一定不能由一条边覆盖，因此最小便覆盖不小于最大独立集。

再构造一种方案：选出所有匹配边，再对于所有未匹配点单独选一条和它相连的边，就得到了一组等于最大独立集的边覆盖，因此结论得证。

有向无环图最小路径覆盖

考虑如下问题：给定简单 DAG，我们要选出其中数目最小的不相交的路径，使得每个点至少在一条路径上。

设给定的有向图为 $G=(V,E)$，构造二分图 $G_0$，左右各 $|V|$ 个点，如果 $(x,y)\in E$，则将左边的点 $x$ 与右边的点 $y$ 连边，有：

定理：$G$ 的最小路径覆盖大小等于 $|V|$ 减去 $G_0$ 的最大匹配大小。

证明：

考虑建立两者之间的对应关系：

对于 $G$ 的一个路径覆盖，对于其中某条路径 $v_1\to\ldots\to v_m$，在 $G_0$ 中选出 $v_i\to v_{i+1}$ 的边，因为路径间不相交，所以每个点入度和出度都不超过 $1$，因此选出的边构成匹配；
对于 $G_0$ 中的一组匹配，同上可以构造 $G$ 的一个路径覆盖，注意没有边经过的点都视为被一条空路径经过。

在上面的对应过程中，每增加 $G_0$ 匹配中的一条边，就有多一条边选入路径覆盖中，而初始视为有 $|V|$ 条路径，每次合并两条，所以合并了 $x$ 次则最小路径覆盖大小就是 $|V|-x$。

例题 $6$：[CTSC 2008] 祭祀

给定简单有向无环图 $G=(V,E)$，求最大的 $A\subseteq V$ 使得 $\forall x,y\in A$，不存在 $x$ 到 $y$ 的路径。

这是一个非常经典的问题。

一个熟知结论是：将 DAG 传递闭包后得到一个偏序集，即如果 $a$ 可达 $b$ 则记 $a\leq b$，显然这确实是个偏序集。

根据 Dilworth 定理，偏序集的最长反链长度等于最小链划分大小，在传递闭包 DAG 上即为：如果选出的满足题目条件的点集 $|A|=m$，则存在 $m$ 条路径可以覆盖 $G$ 中所有点。

因此答案就是传递闭包后的最小路径覆盖大小。

3. 二分图最大权匹配

对于给定二分图 $G=(V,E)$，每条边有一个权值 $w_i$，我们想要找出一组匹配，使得其中包含的所有边权值和最大，称为二分图最大权匹配。

注意，如果给定的 $E$ 不包含所有可能的边，那么最大权匹配不一定是最大匹配。

为了求解这个问题，让我们再次借助线性规划工具：

\[\max \sum\limits_{i=1}^m w_ix_i \]

\[s.t. \begin{cases} \sum\limits_{i=1}^mw(j,i)x_i\leq 1 \\ x_i\ge 0 \end{cases}\]

其中 $w(j,i)$ 表示边 $i$ 是否以点 $j$ 为端点，其实这个问题就是在最大匹配的基础上加上了每条边的权值 $w_i$。

仍旧将它对偶，得到：

\[\min\sum\limits_{j=1}^n y_j \]

\[s.t. \begin{cases} \sum\limits_{j=1}^n w(j,i)y_j\ge w_i \\ y_j\ge 0 \end{cases}\]

我们将对偶问题中的变量 $y_j$ 称为顶点 $j$ 的顶标，那么问题转化成了：

最小顶标和问题：给定二分图，给每个点一个顶标，使得每条边两端点的顶标和不小于边权，且所有点顶标和最小。

不过，再次我们需要做一些补充：

在上面的线性规划证明中，我们要求 $w_i\ge 0$，即边权非负。
但是，如果存在 $w_i<0$，那么就不能用上面的方法证明（顶标有可能是负数，不满足线性规划的条件），我们稍后叙述算法时也将证明：存在 $w_i<0$ 时，下面的算法也能够通过最小顶标和问题解出一种最大权的完美匹配。

接下来我们将介绍 KM 算法，KM 算法通过解决最小顶标和问题，可以求出给定二分图的一组权值和最大的完美匹配。

在叙述算法过程前，先说说怎么将原先的问题（最大权匹配）转化成最大权完美匹配：

如果要求 $w_i\ge 0$ 的最大权匹配，那么我们只需要将所有不存在的边视为边权为 $0$ 的边，如果左右两部点数不相等则补为相等，就转化成了最大权完美匹配问题；
如果要求存在 $w_i<0$ 的最大权完美匹配（当然也可以是权值都非负的），就将不存在的边权值设为 $-\infty$；
如果要求存在 $w_i<0$ 的最大权匹配，那么当然是把所有负权边删掉，变成非负情况。

我们将左部点 $i$ 的顶标称为 $A_i$，右部点 $j$ 的顶标称为 $B_j$，我们要求 $A_i+B_j\ge d(i,j)$，其中 $d(i,j)$ 为 $i,j$ 之间的边权（按照上面的方法补全为完全二分图）。

相等子图定义为所有满足 $A_i+B_j=d(i,j)$ 的边构成的子图。

命题：相等子图中若存在完美匹配，则这组完美匹配是原图的一个最大权完美匹配。

证明：考虑这组完美匹配的边权和，根据相等子图定义应当是 $\sum A_i+\sum B_j$，而对于原图中任意的一组完美匹配，由于 $d(i,j)\leq A_i+B_j$，所以边权和不超过 $\sum A_i+\sum B_j$，所以这组完美匹配是最大的。

接下来考虑：如果相等子图中没有完美匹配，尝试通过调整顶标使得相等子图中的最大匹配变大，从而最终形成完美匹配。

假设此时左侧有点 $x$ 在相等子图的最大匹配中为非匹配点，从 $x$ 开始尝试在相等子图中寻找增广路（由于是最大匹配了所以必然无法找到），然后我们将访问到的左部点顶标减小 $\Delta$，右部点顶标增大 $\Delta$，考虑这样做的影响：

对于匹配边，两边必然都访问到或都不访问到，因此 $A_i+B_j$ 不变，仍然属于相等子图；
对于某个以访问到的左部点为一端的非匹配边，由于 $A_i$ 减小，有可能被新加入相等子图中。

所以这么做不会影响原先匹配，但可以增加新的边进入相等子图，从而继续增广，而我们只要取 $\Delta$ 为所有以左部的被访问到的点为一端的边 $(i,j)$ 中最小的 $A_i+B_j-d(i,j)$ 即可，这样至少加进了一条边（但 $\Delta$ 不能大于这个值，否则不符合顶标的要求）。

于是我们首先任意设定初始合法顶标（如右部点都为 $0$，左部点都为相连边权最大值），每次加入一个左部点，按照上面要求尝试在相等子图中增广，如果成功则直接增大匹配，否则按照上述过程进行顶标调整，直接实现这一算法就得到了基于 DFS 的 KM 算法，复杂度较高。

考虑优化这一算法，我们下面介绍一种 slack 优化的基于 BFS 的 KM 算法。

在每次加入一个左部点，尝试增广时，模拟匈牙利算法求增广路的过程，而对于右部每个点 $y$，记录 $slack_y$ 表示这一轮已经访问的左侧点 $x$ 中，$A_x+B_y-d(x,y)$ 的最小值。
当我们访问到一个左部点时，先用它更新所有右部点的 $slack$ 值，接下来我们取出右部 $slack$ 最小的一个点，将其值设为 $\Delta$，然后将当前已经访问的左部点顶标减小 $\Delta$，当前已访问的右部点顶标增加 $\Delta$，并更新 $slack$ 数组（实际上就是每个点的 $slack$ 也需要减小 $\Delta$）。
下一个访问的左部点将是刚才取出的右部点的匹配点，这就是一个寻找增广路的过程，而当那个右部点是非匹配点时，我们已经找到了一条增广路。
重复上述过程，依次加入所有左部点，最后就求出了最小顶标和问题的解，也就是最大权完美匹配的方案。

例题 $7$：[UVA 1411] Ants

给定平面上 $n$ 个黑点和 $n$ 个白点，请选 $n$ 条线段，每条线段连接一个白点和黑点，每个点只作为一条线段的端点，且这些线段两两不交。

根据简单的初中几何知识，若 $AB\cap CD\ne \varnothing$，则 $AB+CD>AD+BC$。

所以所求的就是连接黑点和白点的长度和最小的 $n$ 条线段对应的匹配，直接执行 KM 算法即可。

4. Hall 定理

对于二分图 $G=(V,E)$，令 $N(v)$ 表示与点 $v$ 相邻的点集，则关于最大匹配，我们有如下结论：

Hall 定理：设二分图 $G$ 的两部分别为 $X,Y$ 且 $|X|\leq |Y|$，则其存在一个大小为 $|X|$ 的匹配当且仅当 $\forall S\subseteq X$，有 $|S|\leq |\bigcup\limits_{v\in S} N(v)|$。

证明：

必要性：若存在 $S$ 使得条件不成立，考虑 $S$ 中所有点的匹配点，形成了一个大小不小于 $|S|$ 的点集，而它们必在 $\bigcup\limits_{v\in S} N(v)$ 中，这说明一个子集的大小大于超集的大小，这是不可能的。

充分性：若条件成立但不存在大小为 $|X|$ 的匹配，则选出左侧一个非匹配点，从其出发进行尝试增广，设访问到的左部点集合为 $L$，右部点集合为 $R$，由于无法成功增广则增广过程中的递归终止点必然在 $L$ 中，考虑递归树，每个 $L$ 中的点的父结点为 $R$ 中的点，则有 $|L|=|R|+1$，而 $R$ 应当是 $L$ 中所有点的 $N$ 的并，这就与条件矛盾。

Hall 定理有一个简单的推论：

推论：若一个无向图每个点度数都为 $k$，则称其为 $k$ 正则图，那么左右点数相等的 $k$ 正则二分图必有完美匹配（$k\ge 1$）。

证明：

考虑一个左部点集 $L$，假设其中所有点邻居并 $R$ 有 $|L|>|R|$，那么 $R$ 中所有点的度数和不小于 $|L|\times k$，但是 $R$ 的大小不到 $|L|$，所以 $R$ 中所有点的度数和是 $|R|\times k<|L|\times k$，因此这是不可能的。

Hall 定理还可以用于点带权值的情况，若左部点 $i$ 需要匹配 $a_i$ 个右部点（可重复），而右部点 $i$ 可匹配 $b_i$ 个左部点（可重复），那么我们只需将定理条件中的 $|S|$ 和 $|\bigcup\limits_{v\in S} N(v)|$ 分别改成其元素和即可。

我们还可以对此定理进行推广：

Hall 定理推广：设二分图 $G$ 的两部分别为 $X,Y$，则其最大匹配为 $|X|-\max(|S|-|\bigcup\limits_{v\in S} N(v)|)$，其中 $S\subseteq X$。

证明：

令 $f(S)=|S|-|\bigcup\limits_{v\in S} N(v)|$。

首先最大匹配不会大于这个数，考虑 $f(S)$ 取到最大的 $S$，其中的点的总匹配数不会超过 $|\bigcup\limits_{v\in S} N(v)|$，所以整张图的最大匹配数不会超过 $|X|-\max(f(S))$。

随后，若最大匹配小于这个数，考虑从左部所有非匹配点出发尝试增广，类似 Hall 定理的证明，可知所有递归过程构成以所有左部非匹配点为根的，所有叶子为左部点的森林，设左部非匹配点有 $s$ 个，那么这个森林中左右部点个数 $l,r$ 满足 $l=r+s$，而 $s$ 是一个 $f(S)$，所以左部非匹配点不超过 $\max(f(S))$ 个。

例题 $8$：

给定左部 $n$ 个点，右部 $m$ 个点的二分图，左部点 $i$ 向右部 $[l_i,r_i]$ 内所有点连边，求是否存在大小为 $n$ 的匹配。

考虑枚举一个右部点集 $R$ 作为 $\bigcup\limits_{v\in S} N(v)$，然后考虑哪些左部点可以在 $S$ 中，也就是算出所有邻居都在 $R$ 中的点的左部点集 $L$。对于确定的 $L$，将 $R$ 拆成若干个两两端点不连续的区间，可以发现每段区间对应了 $L$ 中的邻居是不交的（因为每个 $L$ 中的点对应了邻居是一个区间），那么如果 $|L|>|R|$，则必然是存在一段区间对应的 $R'$ 与其邻居集合 $L'$ 满足 $|L'|>|R'|$。

所以当不存在大小为 $n$ 的匹配时，一定存在一个区间作为 $R$ 使得 Hall 定理的条件不成立，假设我们枚举这个区间 $[l,r]$，就要算出左部满足 $[l_i,r_i]\subseteq [l,r]$ 的 $i$ 的个数，减去 $r-l+1$ 后取 $\max$。

考虑用数据结构维护这一过程，升序扫描 $r$，对每个 $l$ 维护当前 $[l,r]$ 对应的 $|L|-|R|$，$r$ 增大时若有一个 $r_i=r$ 的左部点 $i$，则需将 $l\leq l_i$ 的所有 $l$ 对应的 $|L|-|R|$ 增大 $1$，然后我们每次询问全局最大值，若存在一个正值则不存在大小为 $n$ 的匹配。

例如，线段树就可以实现这一要求，时间复杂度为 $O((n+m)\log m)$。

但是之后，我又得知了这题的一种更简单做法，我们接下来继续分析这张图匹配的特性。

把所有左部点按照 $r_i$ 从小到大排序，考虑第一个左部点 $x$ 应该匹配哪个右部点。

根据 Hall 定理，设左部点集为 $V_L$，对于 $A\subseteq V_L$ 且 $x\notin A$，我们希望删除 $x$ 及其匹配点后对 $\bigcup\limits_{v\in A} N(v)$ 影响尽可能小，也就是说在能使其不变的情况下就使其不变，因此我们考虑一种贪心：选取 $l_x$ 作为 $x$ 的匹配点。

考虑这种匹配的最优性，若匹配后 $\bigcup\limits_{v\in A} N(v)$ 减小了 $1$，则说明 $l_x\in \bigcup\limits_{v\in A} N(v)$，而由于 $r_x$ 是所有 $r_i$ 中最小的，所以若 $l_x\in [l_y,r_y]$ 则对于任意的 $z\in [l_x,r_x]$ 都有 $z\in [l_y,r_y]$，所以不管选取 $[l_x,r_x]$ 中的哪个点都会使得 $\bigcup\limits_{v\in A} N(v)$ 减小 $1$，所以这种决策是不劣的。

因此贪心匹配，每次选取当前点的可匹配点中最靠前的一个没有被匹配过的点，若每个点都能匹配则找到了大小为 $n$ 的匹配。

这启发我们：Hall 定理可以作为一些显式或隐式匹配问题的贪心策略依据。

例题 $9$：

给定左部 $n$ 个点，右部 $m$ 个点的二分图，左部点 $i$ 向右部 $[1,l_i]\cup [r_i,m]$ 内所有点连边，求最大匹配。

枚举左部点集 $L$，其右部点邻居集 $R$ 必然是一段前缀并一段后缀。

考虑枚举 $R=[1,l]\cup [r,n]$，同上题可以得到关于 $L$ 中的点的 $l_i,r_i$ 的限制，还是用数据结构升序扫描 $l$，对每个 $r$ 维护 $|L|-|R|$，当 $l$ 增加时若遇到 $l_i=l$ 的 $i$，则对于 $r\leq r_i$ 的 $r$，其 $|L|-|R|$ 将增大 $1$。

线段树可以做到 $O((n+m)\log m)$ 的时间复杂度。

例题 $10$：

给定左部 $n$ 个点，右部 $m$ 个点的二分图，左部点有点权 $a_i,b_i$，右部点有点权 $c_j,d_j$，且 $(i,j)$ 之间有边当且仅当 $a_i\ge d_j$ 或者 $c_j\ge b_i$，求最大匹配。

考虑左部点 $i$ 会向哪些右部点连边，一种是 $d_j\leq a_i$ 的，一种是 $c_j\ge b_i$ 的，那么和上题一样，我们只需要枚举右部点中 $d_j$ 最小的一段和 $c_j$ 最大的一段的并作为 $R$ 就可以了，维护基本同上题，只是需要在重叠时进行一些处理。

线段树可以做到 $O((n+m)\log m)$ 的时间复杂度。

5. 网络最大流

给定有向图 $G=(V,E)$，每条边有非负容量 $c_i$，同时给定两个相异点 $s,t\in V$ 分别称源点和汇点，则称这是一张网络图。

令 $c(u,v)$ 当 $u,v$ 之间有边时等于这些边的容量和，否则等于 $0$。

定义一个合法流函数 $f:V\times V\to R$ 是满足如下性质的函数：

$f(u,v)\leq c(u,v)$；
$f(u,v)=-f(v,u)$；
令 $fl_i=\sum\limits_{j=1}^n f(i,j)$，有 $fl_s\ge 0,\ fl_t\leq 0$，对于其他点都有 $fl_i=0$。

直观理解：从 $s$ 发出流到达 $t$，沿有向边传播，第一个性质告诉我们每条边有运载流的上限 $c_i$，第二个性质定义了流的方向：负数表示反向流，第三个性质告诉我们除 $s,t$ 外每个点都不储存流，所有流进的流都会流出。

最大流问题即需要对于给定网络图找出一个合法的流函数，使得 $fl_s$（称为流量）最大。

首先让我们证明一些基本性质：

$fl_s=-fl_t$，这一点可通过直接将所有 $f(i,j)$ 相加等于 $0$ 得证；
若不存在 $i\to j$ 和 $j\to i$ 的边，则必有 $f(i,j)=f(j,i)=0$，这是因为 $c(i,j)=c(j,i)=0$。

根据第二条性质，我们只需要记录存在边的点对之间的流，更具体地，只需要记录每条边上运载的流的大小。

下面将介绍解决最大流问题最常用的 Dinic 算法（如果想要搞清楚几种网络流算法的本质，复杂度分析和写法，建议去看其他博客，我这里对于算法本身的讲解可能不太行）。

首先确定一个任意的初始流函数，如所有 $f(i,j)$ 都为 $0$，随后不断尝试扩大最大流。

设当前已有一个流函数 $f$，则取 $c'(i,j)=c(i,j)-f(i,j)$ 为各条边容量得到的新的网络图称为残量网络。

在残量网络上，我们任取一条 $s\to t$ 的路径 $v_1\to \ldots\to v_n\ (v_1=s,v_n=t)$，使得 $c'(v_i,v_{i+1})>0$，则称这是一条增广路。

各种最大流算法几乎都用到了一个重要性质：当前流函数是最大流，当且仅当残量网络不存在增广路，此结论将在接下来介绍最小割问题后再作证明。

一种暴力的思路：每次找出当前残量网络中的一条增广路（直到不存在增广路），考虑其中 $c'(v_i,v_{i+1})$ 的最小值 $m$，将路径上各边的流量增大 $m$，则最大流会增大 $m$，由于最大流有限，所以算法一定会在有限次增广后结束。

Dinic 算法对此进行了优化，在寻找增广路前，先对残量网络进行了分层，使得 $s$ 可达的每个点分配到一个层号，且 $s$ 层号为 $1$，对于任意层数为 $i$ 的点都存在层数为 $i-1$ 的点向它连容量为正的边（$i\ge 2$）。

随后我们在增广过程中，只保留出发点的层数比终点层数恰好小 $1$ 的那些边，这构成了一个 DAG，在 DAG 上从 $s$ 出发搜索增广路，不会成环，当任意一条路径搜索到 $t$ 时即可以接受这条流。

Dinic 算法的优势是一次可多路增广，其中的搜索部分通常采用 DFS 实现，而分层采用 BFS 实现。

Dinic 的一个常见优化是当前弧优化，在 DFS 到一个点时，我们每次都顺序遍历其出边尝试增广，但是一旦一条边的流量已经达到其容量，那么下次就不必再考虑这条边，可以将当前点出边对应的表头指向下一条边。

最大流可以解决二分图最大匹配问题：建立源汇点 $s,t$，从 $s$ 向所有左部点连容量为 $1$ 的边，从所有右部点向 $t$ 连容量为 $1$ 的边，并保留原来二分图中的所有边，容量为 $1$，然后求 $s$ 到 $t$ 的最大流，就是二分图最大匹配的匹配边数，用当前弧优化的 Dinic 算法实现，这种方法快于匈牙利算法。

例题 $11$：[SDOI 2013] 费用流

给定网络图，Alice 需要给出一个最大流对应的流函数，随后 Bob 可以给每条边赋予非负费用 $c_i$，要求所有边费用总和为 $P$，使得 Alice 的最大流中所有边的流量乘费用求和最大，Alice 希望这个最大值最小，求这个最大值的最小值。

显然 Bob 会把 Alice 的最大流中流量最大的一条边的费用设为 $P$，其他边费用设为 $0$。

所以我们二分各边流量的最大值，将所有边的容量对此取 $\min$，然后做最大流，若等于原图最大流则缩小这个值，否则扩大这个值，通过二分答案即可确定流量最大的边的最小流量，也就求出了答案。

例题 $12$：[USACO 07 OPEN] Dining

有 $n$ 头牛，$f$ 种食物和 $d$ 种饮料，每种食物和饮料只有一份，每头牛有一些喜欢的食物和饮料，求最多有多少头牛可以得到自己喜欢的食物和饮料。

令食物为左侧的点，饮料为右侧的点，牛为中部的点，每个牛向所有喜欢的食物和饮料连边，源点向每种食物连容量为 $1$ 的边，每种饮料向汇点连容量为 $1$ 的边，同时为了保证每头牛只能算一次，所以每个牛拆成两个点 $b,b'$，食物连到 $b$，然后 $b'$ 连到饮料，$b$ 到 $b'$ 再连容量为 $1$ 的边，图的最大流即为答案。

最大流问题还可以用于解决一些其他模型。

对于有向图 $G$，每条边有非负代价 $c_i$，求删除代价和最小的一组边集，使得 $s$ 到 $t$ 不连通，此问题称为最小割问题。

定理：最小割等于将每条边的代价转换成其容量后 $s$ 至 $t$ 的最大流。

证明：

首先将网络图中 $s$ 无法到达的点和无法到达 $t$ 的点删去，容易发现这不影响最大流和最小割的值。

接下来我们按如下方法刻画一组割：将 $V$ 拆分为两个不相交子集 $L,R$，使得 $s\in L,t\in R$，然后删除所有 $u\in L,v\in R$ 的 $(u,v)$ 边，可以验证这是 $s,t$ 间的一组割，并且任何一组割都可以找出一组满足该条件的”子割“（具体地，令割后 $S$ 能到达的点集为 $L$，其余点集为 $R$），因此最小割一定出于其中，将这样的割称为 $C(L,R)$。

接下来的证明分成三个部分：

对 $G$ 中的任意合法流函数，其 $fl_s$ 不超过 $G$ 的最小割。

考虑 $L$ 中所有点的 $fl$ 之和，一方面它等于 $fl_s$，另一方面这里面的所有流量都是从 $L$ 到 $R$ 的，所以不能超出 $L$ 到 $R$ 所有边的容量和，即 $C(L,R)$。
最大流对应的残量网络中无增广路。

若有增广路，则还可拓展出更大的流。
若一个流对应了无增广路的残量网络，则它也对应了一个不超过其 $fl_s$ 的割。

考虑将 $L$ 设为残量网络中 $s$（通过容量为正的边）可达的点集，其余点放在 $R$ 中，则 $L$ 到 $R$ 的边必定都是满流的，所以 $fl_s$ 不小于这组割。

同时，根据 $1$ 可知，这个流的流量恰好等于割的大小。

由此，我们证明下面三个命题等价：

$G$ 中存在一组割 $C(L,R)$ 等于 $G$ 中合法流函数 $f$ 的流量；
$G$ 中的流函数 $f$ 是最大流；
$G$ 中关于 $f$ 的残量网络是无增广路的。

所以任何最大流可以得到一组最小割，而最小割大小又不小于最大流流量，因此最小割大小等于最大流流量。

同时我们还可以的得到刚才要证的一个结论：无增广路的残量网络必然对应最大流。

因此我们只需求出 $G$ 中从 $s$ 到 $t$ 的最大流，就可以求出 $s,t$ 间的最小割了。

这种给定源点汇点的最小割问题称为 $s-t$ 最小割，而对于无向图，还可以定义其全局最小割，Stoer-Wagner 算法可以在 $O(n^3)$ 的时间复杂度内解决这个问题，但这和网络流关系不大。

例题 $13$：[USACO 5.4] Telecowmunication

给定无向图 $G$ 和点 $s,t$，求最少删除多少个非 $s,t$ 的点可以使得 $s$ 到 $t$ 不连通。

按照上一道例题的方法，我们将每个点拆成两个点 $x_u,y_u$，从 $x_u$ 到 $y_u$ 连代价为 $1$ 的边，若原图有边 $(u,v)$ 则连 $(y_u,x_v)$，$(y_v,x_u)$，代价都是 $+\infty$，此图的最小割即为答案。

注意当我们要求一条边不能被割时，就将代价设为 $+\infty$。

给定有向图 $G$，每个点有可负点权 $a_i$，选出点集的子集 $A$，满足若 $u\in A,\ (u,v)\in E$ 则 $v\in A$，求 $\sum\limits_{u\in A}a_u$ 的最大值，这个问题称为最大权闭合子图问题。

考虑转化问题，我们可以选择一些点权非负的点，但是需要付出的代价是它们能够到达的所有点权为负的点的点权，这样转化的好处是：如果一个点权为正的点可以到达一个点权为正的点，那么根据和最大的原则，若选了前者则也会选后者。

选择一个点权为负的点相当于把答案减掉它的权值，可以理解成我们需要“舍弃”这个点的权值。

因此我们将问题转化成了类似二分图的问题：将点权非负的点向它能到达的所有点权为负的点连边，再从 $s$ 向点权非负的点分别连边，点权为负的点向 $t$ 连边，那么考虑一种选择对应了什么：

对于一个点权非负的点，要么干脆不选它，要是选了就得舍弃它能到达的所有点权为负的点的点权；
如果不选这个点，就理解成割掉 $s$ 到它的边，而舍弃一个右边的点就理解成割掉它到 $t$ 的边，由此，一种选择对应一种割；
将 $s$ 到点权非负的点的边的代价设为其权值，点权为负的点到 $t$ 的边的代价设为其权值的绝对值，其余边代价为 $+\infty$，用点权非负的所有点的权值和减去 $s$ 到 $t$ 的最小割即为答案。

在熟悉最大流后，下面集中讨论一些二分图和网络流问题中构造方案以及所有方案的交并的问题。

最大流方案

做完 Dinic 算法外我们已经得到了每条边的流量，这就是一种方案。

最小割方案与可行边必经边

根据我们证明最大流最小割定理时所用的方法，求出最大流后顺便（在最后一次不成功的 BFS 中）算出当前残量网络中 $s$ 能到达的所有点，设这个集合为 $L$，其他点构成的集合为 $R$，则对于边 $(u,v)$，如果 $u\in L$ 且 $v\in R$，那么 $(u,v)$ 在最小割中，这构成了最小割的一种方案。

最小割可行边定义为存在一种最小割使得这条边被割断，必经边定义为每个最小割中这条边都被割断。

首先考虑简单的判断，设原图为 $G$，删掉的边为 $u\to v$ 的代价为 $w$ 的边，那么：

此边是可行边，当且仅当图 $G$ 中删除这条边（代价改为 $0$）后的图的最小割减少了 $w$；
此边是必经边，当且仅当图 $G$ 中把这条边代价改为 $+\infty$ 后的图的最小割变大。

但是这样似乎并不够快，在 $G$ 求完最大流后的残量网络 $G'$ 上讨论问题（只保留容量非 $0$ 的边），我们下面给出更强的结论：

命题：一条边 $(u,v,w)$ 是最小割可行边，当且仅当这条边满流，并且 $G'$ 上不存在 $u\to v$ 的路径。

证明：

如果这条边不满流，那么直接删掉这条边，退掉 $s\to u$ 和 $v\to t$ 的等量的流，整个网络的流量减少了这条边的当前流量，不到 $w$，根据上面的结论这不是可行边；
如果存在 $u\to v$ 的路径，那么删除这条边后还能找到 $s\to u\to v\to t$ 的增广路，故最大流减少了不到 $w$，根据上面的结论这不是可行边；
如果这条边满流且不存在 $u\to v$ 的路径，则删除这条边后仍然不存在 $s\to t$ 的增广路，故最大流减少了恰好 $w$。

命题：一条边 $(u,v,w)$ 是最小割必经边，当且仅当这条边满流，并且 $G'$ 上存在 $s\to u$ 和 $v\to t$ 的路径。

证明：

如果这条边不满流，那么直接按照之前说的方案构造一组最小割，就不会包含这条边；
如果 $G'$ 中不存在 $s\to u$ 的路径，那么加大这条边的容量，因为找不到 $s\to u$ 的路径，所以最大流不会变大，从而最小割也不会变大，根据上面的结论不是必经边；
如果 $G'$ 中不存在 $v\to t$ 的路径，同理；
如果这些条件都满足，那么将这条边的容量改为 $+\infty$ 后可以找到 $s\to u\to v\to t$ 的增广路，从而最小割增大，这是必经边。

下面归纳一下这两个命题，并给出一种实现方法：

定理：将 $G'$ 进行 SCC 缩点，则边 $(u,v,w)$ 是可行边当且仅当满流且 $u,v$ 在不同强连通分量，是必经边当且仅当满流且 $s,u$ 在同一强连通分量，且 $v,t$ 在同一强连通分量。

证明：以下都设探讨的边满流。

假设存在 $u\to v$ 的路径，又由于满流所以这条边的逆向边 $(v,u,0)$ 也在 $G'$ 中容量非零，所以有环 $u\to v\to u$，即 $u,v$ 在同一 SCC；反之，假设不存在 $u\to v$ 的合法路径，那么它们肯定不在同一 SCC。

因此对于满流边 $(u,v,w)\ (w>0)$，存在 $u\to v$ 路径当且仅当 $u,v$ 在同一 SCC，那么它是可行边就等价于不在同一 SCC 了。

假设存在 $s\to u$ 的路径，那么由于这条边满流，所以 $u$ 有入流量，因此可以找到 $s\to u$ 的一条流，将其反过来就得到 $G'$ 中 $u\to s$ 的路径，因此 $s,u$ 在同一 SCC；反之 $s,u$ 肯定不在同一 SCC；同理 $v,t$。

因此对于满流边 $(u,v,w)\ (w>0)$，它是必经边等价于存在 $s\to u,\ v\to t$ 的合法路径，二者分别等价于一组同一 SCC 的关系。

因此命题得证。

现在可以试探讨最小割方案的结构：将 $G'$ 进行缩点后得到 DAG，连接不同 SCC 的满流边是可行边，从 $s$ 所在 SCC 连到 $t$ 所在 SCC 的满流边是必经边，而从 $s$ 所在 SCC 连出去的边构成了最小割的一种方案（就是最开始讲的那种）。

二分图最大匹配方案与可行边（点）必经边（点）

二分图最大匹配方案可以用网络流或匈牙利算法直接求出，接下来考虑求可行边与必经边。

定义：如果一条路径依次通过非匹配边和匹配边，首尾分别是匹配边和非匹配边，并且终点是非匹配点，那么就称这是一条半增广路。

定义：如果一个简单环依次通过非匹配边和匹配边，那么就称这是一条增广环。

考虑半增广路和增广环的实际意义：如果我们将半增广路或增广环上所有边的状态（是否是匹配边）取反，可以得到一个新的最大匹配。

并且倒过来也可以成立：

定理：对于任意两组最大匹配 $P_1,P_2$，总存在一种方法，使得进行若干次取反半增广路或取反增广环的操作，使 $P_1$ 变成 $P_2$。

证明：类似证明无增广路等价于最大匹配的思路，我们求出两个匹配的对称差的导出子图 $T=P_1\Delta P_2$。

由于 $P_1,P_2$ 是匹配，所以 $T$ 中点的度数不大于 $2$，所以 $T$ 是由若干链和环组成的。

长度为奇数的链是不可能存在的——否则这就是其中一个匹配（这条链首尾不属于的那个匹配）的一条增广路。

因此只有偶链和环，而它们就分别是上面所说的半增广路和增广环，将它们分别取反即可从 $P_1$ 变为 $P_2$。

接下来将这一结论运用到求可行边与必经边上来，首先任求一个最大匹配 $P$，然后我们分别有：

命题：边 $(u,v)$ 是二分图最大匹配的可行边，当且仅当 $(u,v)$ 属于当前最大匹配或存在一条经过 $(u,v)$ 的半增广路或增广环。

证明：

如果 $(u,v)$ 属于当前最大匹配，那么毋庸置疑其是一条可行边。
如果 $(u,v)$ 不属于当前最大匹配但存在经过 $(u,v)$ 的半增广路或增广环，将之取反即得到一组包含 $(u,v)$ 的匹配。
如果 $(u,v)$ 不属于当前最大匹配且不存在经过 $(u,v)$ 的半增广路和增广环，假设存在最大匹配 $P'$ 包含 $(u,v)$，则 $P\Delta P'$ 中没有任何一条包含 $(u,v)$ 的增广路，半增广路和增广环，这是不可能的。

命题：边 $(u,v)$ 是二分图最大匹配的必经边，当且仅当 $(u,v)$ 属于当前最大匹配且不存在一条经过 $(u,v)$ 的半增广路或增广环。

证明：

如果 $(u,v)$ 不属于当前最大匹配，那么当然不是必经边。
如果 $(u,v)$ 属于当前最大匹配但有一条经过它的半增广路或增广环，将之取反即得到不包含 $(u,v)$ 的匹配。
如果 $(u,v)$ 属于当前最大匹配且没有经过它的半增广路或增广环，假设存在最大匹配 $P'$ 不包含 $(u,v)$，则 $P\Delta P'$ 中没有任何一条包含 $(u,v)$ 的增广路，半增广路和增广环，这是不可能的。

在更进一步之前，我们先考虑将半增广路也转换成增广环，考虑到半增广路的两端分别是匹配点和非匹配点，我们模仿网络流求解二分图时那样进行如下建图：

建立源点 $s$ 和汇点 $t$，从 $s$ 向左部非匹配点连边，左部匹配点向 $s$ 连边；从 $t$ 向右部匹配点连边，右部非匹配点向 $t$ 连边；
对于原二分图中的边，如果属于当前最大匹配，就从右部点连向左部点，否则就从左部点连向右部点。

考虑新图，一条不经过 $s,t$ 的路径必然是交替出现匹配边和非匹配边的，而一个不经过 $s,t$ 的环就是增广环。

再考虑经过 $s,t$ 的环，例如经过 $s$ 的一个环，其实就对应了环上与 $s$ 相邻的一对匹配点和非匹配点之间的半增广路。

所以在新的有向图 $G'$ 中，一个简单环就对应了原来的一个增广环或半增广路，也就是说包含一条边的增广环或半增广路存在等价于这条边的两端在同一 SCC 中。

那么我们可以将上面的命题整理：

定理：边 $(u,v)$ 是二分图最大匹配的可行边，当且仅当它属于当前匹配或 $u,v$ 属于 $G'$ 中同一 SCC，而边 $(u,v)$ 是二分图最大匹配的必经边，当且仅当它属于当前匹配且 $u,v$ 不属于 $G'$ 中同一 SCC。

值得一提的是，上面的 $G'$ 其实就是网络流建图求二分图匹配后的残量网络。

Bonus：二分图最大匹配可行点？

任何度数不为 $0$ 的点都是可行点，考虑随便选择一条出边，就能找到长度至少为 $2$ 的半增广路。

Bonus：二分图最大匹配必经点？

仿照上面的结论，只要不存在以这个点为端点的半增广路，也就是不存在包含它到 $s$ 的边的环，也就是它和 $s$ 不属于同一强连通分量。

6. 最小费用最大流

给定一张网络图，每对点除容量 $c(u,v)$ 外还有价值函数 $w(u,v)$，求一个流函数 $f(u,v)$，使得源点流量最大的情况下， $\sum w(u,v)\times f(u,v)$ 最小，这个问题称为最小费用最大流，简称费用流。

请注意，我们下面讨论的是价值函数不构成负圈的网络图上的费用流问题，而有负圈的情形将在介绍上下界网络流后说明。

首先我们补充一下残量网络的定义：残量网络中每条反向边价值为正向边的相反数，这符合反悔的实际意义。

令 $F_i$ 表示流大小为 $i$ 时的最小费用，我们考虑如下算法：

令 $F_0=0$；
在第 $i$ 轮，以价值为边权，找出当前残量网络上 $s\to t$ 的最短路，将其附上 $1$ 的流，并令 $F_i=F_{i-1}+l$，其中 $l$ 是这条路径上所有边价值和。

下面简要地证明其正确性：

归纳证明，当 $n=0$ 时因图不存在负环所以有 $F_0=0$ 是最小的费用；

当 $n\ge 1$ 时，假设结论对 $m<n$ 都成立，若存在一个更小的费用 $F'_{n}$，那么考虑 $F_{n-1}$ 增广到 $F'_n$ 的过程，由于 $F_n$ 已经是增广了最短路的结果，所以 $F'_n$ 中只能是增广了一个负环，但这说明 $F_{n-1}$ 中可以增广这个负环（但倘若这个负环是在 $F'_n$ 增广过程中才出现的，那么就可以与之前增广的某条路径做对称差得到一条更小路径，从而可以消除），$F_{n-1}$ 不是最小的，这与假设矛盾。

如此，我们需要寻找 $f$ 次最短路（其中 $f$ 是最大流流量），在一般题目中都是过不去的，能不能潜在地减少一些增广次数呢？

答案是肯定的，我们有：

命题：在 $F_i$ 的残量网络上找到最短路，若路上所有边的最小容量大于 $1$，则 $F_{i+1}$ 的残量网络上该路径也是最短路。

证明：

假设不是，那么只能是 $F_{i+1}$ 的残量网络最短路经过了一条这条路径上边的反向边。

设其中第一条这样的反向边为 $u\to v$，价值为 $w$，那么我们先找了一段 $s\to u$ 的原先就有的路径，价值和为 $w_1$，然后经过 $-w$ 的代价到达 $v$；再考虑 $F_i$ 中最短路从 $s$ 到 $v$ 的一段，价值和为 $w_2$，那么 $w_2<w_1-w$，所以 $w_2+w<w_1$，所以原先 $s\to u$ 的那段不是最短的，矛盾了。

有了这一命题，我们只要找到一条最短路，就可以连续增广 $x$ 次，其中 $x$ 是这条路径上最小容量。

关于最短路，我们可以直接使用 Bellman-Ford 进行求解。

但也有另一种选择，考虑 Dijkstra 不能直接做的原因：残量网络中可能存在负权边。

那么我们只需要仿照 Johnson 算法，为每个点赋一个势 $h_u$，且满足 $h_u+w(u,v)-h_v\ge 0$，那么取这个正值为新的边权就可以使用 Dijkstra 算法了：

初始时可以用单次 Bellman-Ford 算出初始势，随后我们在每次求解最短路后更新势：
每次的新势本应等于上一次的最短路，但是由于上一次的最短路是带着势算出的，所以我们应在原本的势上累加这个最短路，即每次令 $h'_u\leftarrow h_u+dis_u$。

这样，Dijkstra 也可以用于求解费用流问题了。

上述的费用流算法称为 SSP（Successive Shortest Path）算法，该算法不仅可以求最大流时的最小费用，而且可以求出流量依次为 $0,1,\ldots,f$ 时的最小费用，但前提是无负环。

当要求最大费用时，只需将边权取反并求最小费用即可，而存在负环的最小费用流可以利用后面的上下界网络流解决。

费用流可以用于解决二分图最大权最大匹配，只需将最大流求最大匹配时中间的边附上权值作为价值即可，但其复杂度比 KM 算法高，一般不推荐使用（费用流可以求解大小为 $i$ 的匹配的最大权值，但 KM 应该也可以，如果我会了可能会补上来）。

例题 $14$：[ZJOI 2010] 网络扩容（第二问）

给定一个网络图，每条边有费用 $w(u,v)$，表示让 $u\to v$ 的容量加 $1$ 需要付出 $w(u,v)$ 的代价，求使得 $1\to n$ 最大流增大 $k$ 的最小代价。

新算出最大流 $f$，为了保证新的最大流增大了 $k$，建立新源点 $s$ 向 $1$ 连 $f+k$ 容量的边。

对于原图中每条边 $(u,v,c)$，令其价值为 $0$，并新建 $u\to v$ 的价值为 $w$，容量为 $+\infty$ 的边，表示多流 $1$ 的流就会付出 $w$ 的代价。

新图的最小费用最大流即答案，注意只要 $1\to n$ 连通，那么 $s\to 1$ 的边必定能满流，因为后面的边都附加了 $+\infty$ 的流量。

有一类费用流问题由于图的特殊性，可以使用一类特殊贪心来解决，这种方法通常称为模拟费用流。

由于作者认为模拟费用流和网络流关系较小，所以这里仅稍作提及，也主要是讲和流有关的部分。

费用流这种每次选取一条最短路进行增广的想法让我们联想到贪心，但保证费用流正确性的是其反悔机制——反向边用于退掉之前更劣的流，因此我们考虑在贪心中也贯彻这一点。

例题 $15$：[NEERC 2016] Mole Tunnels

给定 $n$ 个点的完全二叉树，点 $i$ 有 $c_i$ 份食物，接下来依次来了 $m$ 个鼹鼠，第 $i$ 个鼹鼠出现在点 $p_i$，每个鼹鼠要到一个点去，使得每个点的食物数不小于待在这里的鼹鼠数，对每个 $i\leq m$ 计算只考虑前 $i$ 只鼹鼠的最小移动总距离。

$O((n+m)\log n)$。

考虑费用流建图：

从源点向每个鼹鼠所在点建容量为 $1$，价值为 $0$ 的边（一个鼹鼠从 $s$ 来了），树上每条边都是双向的，容量无穷大，价值为 $1$（鼹鼠走过来了），从树上每个点向汇点连容量为食物数量，价值为 $0$ 的边（鼹鼠到地方了）。

下面用贪心来模拟费用流过程：

考虑按照输入的鼹鼠顺序进行增广，按照最短路原则，对于每个鼹鼠都找到当前残量网络中离它最近的那个有食物的点钻进去就行了。

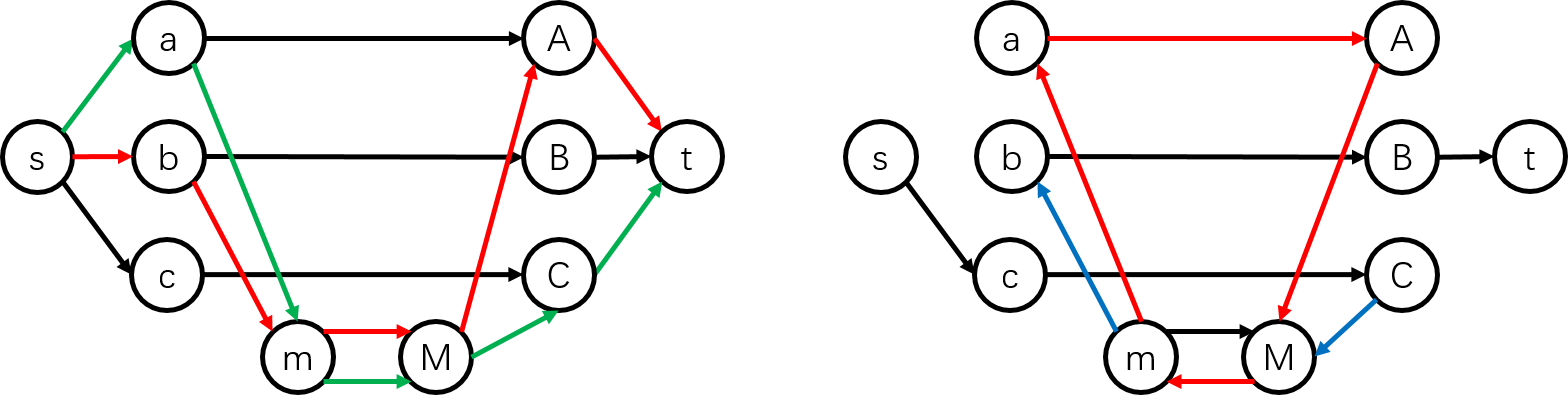
如下图过程，图中非源汇的点中的数字表示当前食物数量，它们之间的黑边表示价值为 $1$ 的边，蓝边表示价值为 $-1$ 的边，红边表示这次的最短路（中图中一条蓝边也在其中），两个鼹鼠依次进行增广的情形如图：

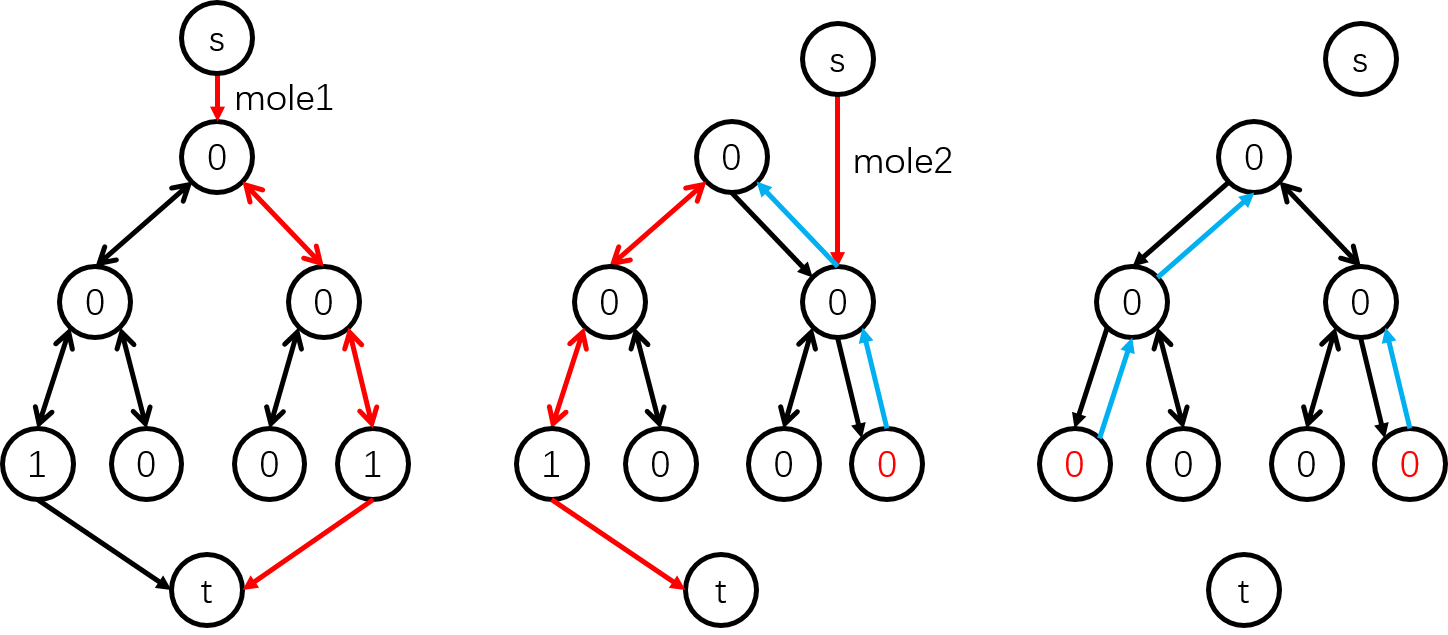
第一个鼹鼠来到根结点，首先找到离它最近的有食物的点（找到了最右边的点），然后走这条流，经过的树边由于有了流量，所以残量网络上就有了反向边（蓝边），代价为 $-1$。

第二个鼹鼠来到根结点右儿子，此时只有最左边的点有食物，它可以跑过去，途经的价值和为 $1$（一条蓝边和一条红边抵消），最终由于根结点与右儿子的蓝边被走过了，下一次的残量网络上又不存在这条边了。

考虑蓝边的实际意义：当第二个鼹鼠来之后，我们发现第一个鼹鼠的决策错误了，应该第一个鼹鼠到左边，第二个到右边才是最优的，所以蓝边给我们提供了一次后悔机会——如果把原来第一个鼹鼠走的那段路换成第二个鼹鼠的，那么这条边就可以退掉了。

由此可以考虑贪心：对于每个鼹鼠都找当前树上离它最近的一个有食物的点，答案增加这条路径的长度，将那个点的食物数量减少 $1$，并将这条路径上所有反向边的边权取反（原来是 $1$ 就变成 $-1$，原来是 $-1$ 就变回 $1$）。

由于完全二叉树的树高为 $O(\log n)$，所以直接采用树形 DP 维护这一过程，每次取反边权只需要将路径上涉及到的点及其祖先的 DP 值进行更新，所以复杂度是 $O((n+m)\log n)$ 的。

例题 $16$：种树

有 $n$ 个排成一排的坑，要在其中恰好 $m$ 个坑里种树，使得不存在两个相邻的坑都有树，每个坑有个美观度 $A_i$，求种上树的坑的美观度之和的最大值。

$O((n+m)\log n)$

设在坑 $i$ 种一棵树，称这棵树占据了位置 $i$ 和位置 $i+1$，那么不存在相邻两个坑有树就等价于每个位置只被占据一次。

因此可以建出一个二分图最大权匹配的模型：以编号为奇数的位置为左部，偶数的位置为右部，$i$ 与 $i+1$ 间连权值为 $A_i$ 的边，其最大权的大小为 $m$ 的匹配就是答案。

可以发现，一条增广路肯定是由一个区间内的坑构成的，相当于我们每次行完一条流，就把三条边合并为了一条边（作为增广路是一个整体），如图：

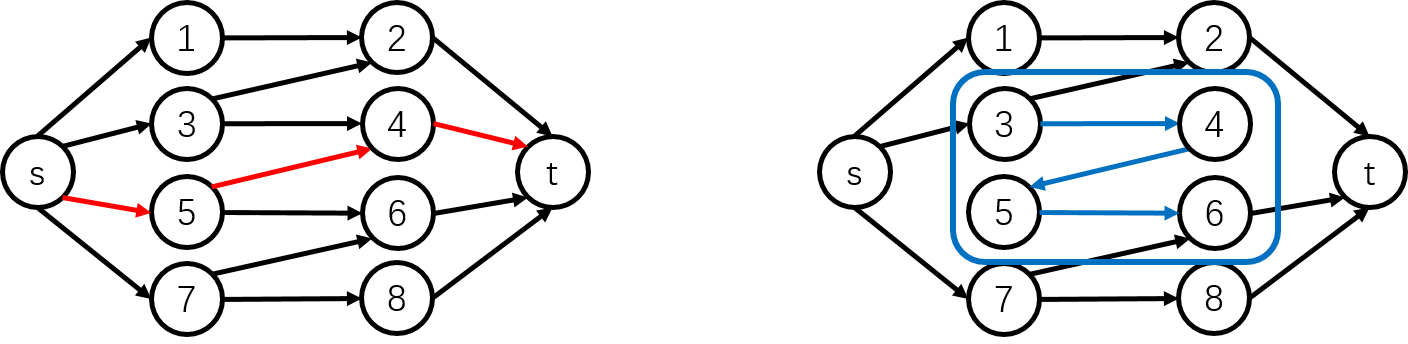
而这个等效边的流量，相当于原来两侧的坑的美观度减掉中间的坑的美观度（因为中间的是反向边）。

因此贪心策略就明显了：每次选择当前美观度最大的坑 $i$，然后删除 $i-1,i,i+1$ 这三个坑，在这三个坑的位置加入一个美观度为 $A_{i-1}+A_{i+1}-A_i$ 的坑。

用堆维护，时间复杂度为 $O((n+m)\log n)$。

例题 $17$：[CF 280 D] k-Maximum Subsequence Sum

维护一个序列 $A$，$q$ 次操作和查询，包括单点修改和询问：从区间 $[l,r]$ 中选出至多 $k$ 个不交子区间的最大元素总和。

$O((|A|+\sum k)\log |A|)$。

考虑给定一个序列，询问 $k$ 段最大子段和怎么做。

费用流建图，从 $i$ 向 $i+1$ 连价值为 $A_i$，容量为 $1$ 的边，$s$ 向每个点，每个点向 $t$ 连价值为 $0$，容量为 $1$ 的边，此时流量恰为 $k$ 的最大费用即为答案。

这个问题中的反悔非常容易理解：就是把选了的区间中的数都改成相反数，这样以后取到的时候表示去掉这个部分。

所以这题的贪心策略也非常显然了：每次选择和最大的子段，将其和加入答案，并将这个区间取反，连续做 $k$ 次后就得到了答案。

利用线段树维护上述操作，时间复杂度为 $O((|A|+\sum k)\log |A|)$。

例题 $18$：[NOI 2019] 序列

给定两个长度为 $n$ 的序列 $a,b$，请从中各选出 $K$ 个下标，使得至少 $L$ 个下标在两个序列里都被选，且两个序列中各自选到的下标对应的数之和最大。

$O(n\log n)$。

首先考虑用费用流解决：

如图，$a,b$ 表示第一个序列中元素，$A,B$ 表示第二个序列中元素，$s$ 向 $a,b$ 连边的价值为这个元素的值（容量为 $1$），$A,B$ 到 $t$ 同理，并从 $a$ 到 $A$（它们在两个序列中下标相同）之间连容量为 $1$ 的边，表示选择一个相同的下标，而新建一个中转点 $M$ 接收不同下标的值，因为这样的值只能有 $K-L$ 个，所以将 $M$ 拆点，两个点之间连容量为 $K-L$ 的边，流量为 $K$ 的最大权匹配即为答案：

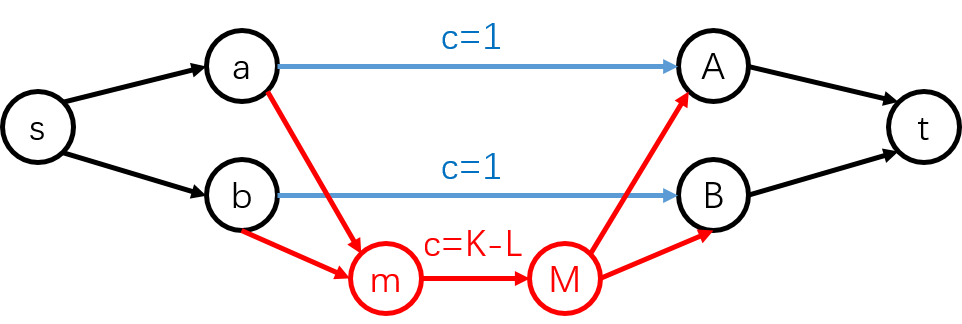
走红边表示不同的下标，走蓝边表示相同的下标，这些边的价值都为 $0$。

下面我们将这个问题中的流分成以下这些类型：

自由流：形如 $s\to a\to m\to M\to B\to t$ 的流；
限制流：形如 $s\to a\to A\to t$ 的流；
反悔流：形如 $s\to a\to A\to M\to C\to t$ 的流。

这样的流如何产生呢？见下图（省去了连向 $m,M$ 的无用边），我们首先流了一次 $b\to A$ 的自由流，然后现在就有了 $A\to M$ 的反向反悔边，所以我们可以利用这条边反悔 $b\to A$ 的匹配，改成一个 $b\to C$，这样 $A$ 就可以与 $a$ 匹配，不改变 $m\to M$ 的流量而进行了一次反悔。

注意这样的反悔有两种，一种是上面说的，还有一种是形如 $s\to a\to m\to c\to C\to t$，即经过 $m$ 进行一次反悔；
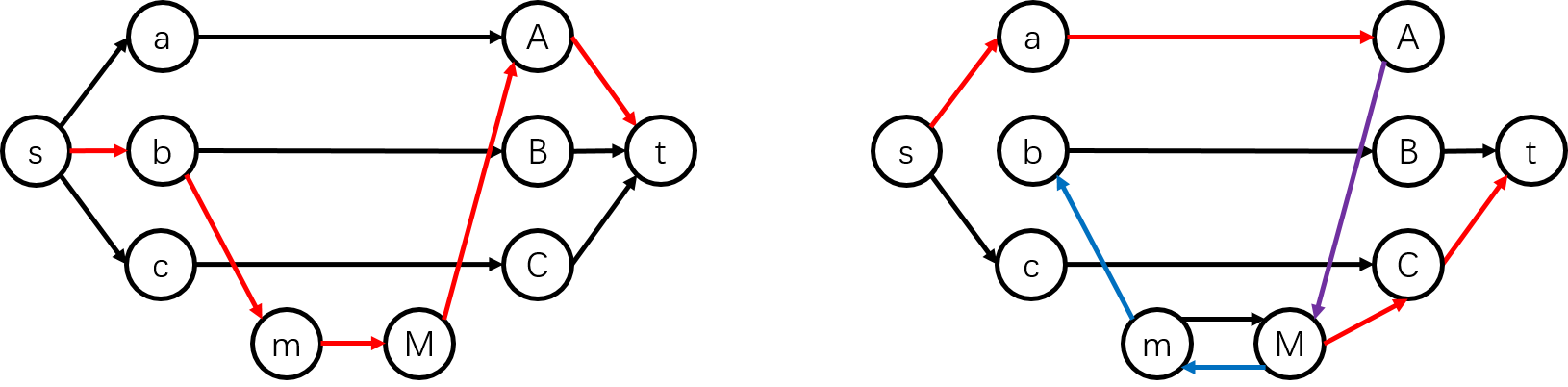
假自由流：形如 $m\to a\to A\to M$ 的流。

见下图（省去了连向 $m,M$ 的无用边），我们首先流了两条自由流 $a\to C$ 和 $b\to A$，随后发现如果我们把 $a\to A\to M\to m\to a$ 这个环上的一条流退掉，就会使自由流的容量增大 $1$，下次要流自由流的时候就不用走 $m\to M$，而是可以借道 $a\to A$。

本质上，这种流的作用是把 $a\to C,\ b\to A$ 换成了 $a\to A,\ b\to C$，使得用掉的自由流变少了。

所以我们在贪心中有如下这些对应的决策：

选择当前最大的一对没有流过的 $a_i,b_j$，如果 $i=j$ 则流限制流，否则流自由流；
选择当前最大的两边都没流过的 $a_i+b_i$，流一条限制流；
选择当前 $b_i$ 已经流过的 $a_i$ 的最大值，以及当前还没流过的 $b_j$ 的最大值，在它们之间流一条反悔流；
选择当前 $a_i$ 已经流过的 $b_i$ 的最大值，以及当前还没流过的 $a_i$ 的最大值，在它们之间流一条反悔流；
每次建立一条流后，都检查是否存在假自由流（环），如果存在就退掉这环上的一条流。

我们只需要记录当前自由流的剩余流量，当选择一条自由流时流量减少 $1$，退掉一个假自由环时流量增加 $1$，然后用堆维护四种决策即可。

注意当某些决策同样优时，选择能增大自由流剩余流量的。

时间复杂度为 $O(n\log n)$。

7. 上下界网络流

现在将网络图的定义做一些调整，除了流量上限（容量）$c(u,v)$ 外，每对点还存在流量下限 $b(u,v)$，此时的流函数 $f(u,v)$ 在满足之前提到的性质的基础上，还应该满足 $b(u,v)\leq f(u,v)\leq c(u,v)$，将这样的问题统称为上下界网络流。

上下界网络流还可以按一些标准分类：

无源汇和有源汇：因为有了上下界，有些题目中可以只保留流量守恒的限制，而没有源汇点 $s,t$，这类问题是无源汇上下界网络流问题；
可行流，最大流，最小流，费用流等。

本篇中基本都会提到这些类问题。

无源汇上下界可行流

最基础的上下界网络流问题：给定一张上下界网络图，求一种合法的流量函数，使得每个点都满足流量守恒。

考虑将问题转化成无下界的，我们熟悉的网络流问题。

首先我们强制每条边都要流到下界，即 $f'(u,v)=b(u,v)$，令 $c'(u,v)=c(u,v)-b(u,v)$，此时一个点的出入流量差为 $f_u=\sum b(u,i)-\sum b(i,u)$，然而这可能是不满足流量守恒的。

对于一个 $f_u>0$ 的点 $u$，它的出流量太多了，所以需要等同于 $f_u$ 的入流量来抵消他，如何创造这个入流量呢？既然有入就要有出，所以我们从 $u$ 向外界连一条容量恰好为 $f_u$ 的边，这条边就可以”吸收”掉 $f_u$ 的入流量，使得 $u$ 满足流量守恒了。

对于一个 $f_u<0$ 的点 $u$，同样的，为了抵消掉多出的入流量就需要等同于 $-f_u$ 的出流量，而只要从外界连向 $u$ 一条容量恰好为 $-f_u$ 的边，就可以创造出这个同等大小的出流量，使得 $u$ 满足流量守恒了。

因此，我们新建超级源汇 $S,T$，对于 $f_u>0$ 的点向 $T$ 连容量为 $f_u$ 的边，对于 $f_u<0$ 的点从 $S$ 向它连容量为 $-f_u$ 的边，并将其他原图中就有的边的容量设为 $c'(u,v)=c(u,v)-b(u,v)$。

根据 $\sum f_u=0$ 可以知道 $S$ 的出容量等于 $T$ 的入容量（设为 $F$），而只有这些边全都满流才能满足流量守恒，所以我们算 $S$ 到 $T$ 的最大流，如果恰好等于 $F$ 则可行流存在，且残量网络上的容量就是 $c(u,v)-f(u,v)$ 的值；如果最大流小于 $F$，则可行流不存在。

有源汇上下界可行流

上一个问题略微修改一下：给定一张有源点汇点的上下界网络图，求一种合法的流量函数。

考虑将问题转化成无源汇上下界可行流。

有源汇和无源汇的区别不过在于 $s$ 可以满足 $f_s>0$，而 $t$ 可以满足 $f_t<0$，但 $f_t=-f_s$，所以只要我们从 $t$ 向 $s$ 连一条容量 $+\infty$ 的边后，就可以转化成无源汇问题了。

有源汇上下界最大流

首先求一次有源汇上下界可行流，假如不存在则无解。

记录 $t\to s$ 边的流量，这就是当前 $s\to t$ 的流量。

因为现在和 $S,T$ 相等的边肯定都满流了，所以这两个点已经没用了，下界也没用了，我们只需要在当前的残量网络上做一次普通的 $s\to t$ 的最大流再加上刚才求可行流时的答案即可（实现时可以删掉 $t\to s$ 的边，也可以不删，如果不删那么算出来的直接就是最大流）。

另一思路：二分答案 $m$，将 $t\to s$ 边下界设为 $m$ 看是否存在可行流。

有源汇上下界最小流

同上先求可行流，记录当前 $s\to t$ 的流量。

原来我们要求最大流，不断从 $s$ 到 $t$ 找增广路，现在只是反过来，为了退流而不断从 $t$ 到 $s$ 找增广路，找到一条就退掉一条。

更本质地说，用当前流量减掉残量网络上 $t\to s$ 的最大流，就是 $s\to t$ 的最小流了。

同最大流，也可以二分答案来做。

无源汇上下界最小费用可行流

按照无源汇上下界可行流同样建图，新增的边价值为 $0$。

先将初始费用设为 $\sum b(u,v)\times w(u,v)$，然后做 $S\to T$ 的最小费用最大流，其费用即为答案。

有源汇上下界最小费用流

关于有源汇上下界最小费用可行流，就是连边 $t\to s$ 后变为无源汇情况，和之前的转化是一样的。

而如果是最小费用最大流，其实也一样，跑完 $S\to T$ 的最小费用最大流后再跑 $s\to t$ 的最小费用最大流即可。

这里最大流改成最小流，最小费用改成最大费用也都一样，只是前面各种 trick 的互相组合，这里不再赘述。

有负环的费用流

对于一条价值为负数的边 $(u,v,c,w)$，我们先假设这条边流满，即答案费用加上 $w\times c$，然后建反边 $(v,u,c,-w)$ 用于退流，此时就全是正权边了！

但是这有一个问题，现在的 $u,v$ 可能不满足流量守恒，但是前面所说的上下界网络流的基本思路和这里是一样的，我们只需要建立超级源汇 $S,T$，从 $S$ 向入流量过多的点连边，出流量过多的点向 $T$ 连边。

如果原问题无源汇，那么现在就是个 $S\to T$ 的正权费用流；如果原问题有源汇，就建边 $t\to s$，跑完 $S\to T$ 后再跑 $s\to t$；如果原问题有上下界，和这个方法也是兼容的。

例题 $19$：[Luogu P4843] 清理雪道

给定 DAG，求最少需要几条路径能覆盖所有边至少一次。

类似于前面说的最小路径覆盖，只是现在可以交了，仍然可以用网络流模型解决。

对于每一条路径 $a\to b$，看成是一条流 $s\to a\to b\to t$，也就是从 $s$ 向所有点，所有点向 $t$ 连容量区间为 $[0,+\infty]$ 的边，而为了保证每条边至少被覆盖一次，原图中边的容量区间是 $[1,+\infty]$，路径数量最少，即有源汇上下界最小流。

这样将覆盖转化为下界的思路比较通用。

8. 网络流扩展与建模举例

标签：二分,匹配,最大,增广,路径,最小,复习,NOI
来源： https://www.cnblogs.com/ix35/p/14718776.html

本站声明： 1. iCode9 技术分享网（下文简称本站）提供的所有内容，仅供技术学习、探讨和分享；
2. 关于本站的所有留言、评论、转载及引用，纯属内容发起人的个人观点，与本站观点和立场无关；
3. 关于本站的所有言论和文字，纯属内容发起人的个人观点，与本站观点和立场无关；
4. 本站文章均是网友提供，不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属；如您发现该文章侵犯了您的权益，可联系我们第一时间进行删除；
5. 本站为非盈利性的个人网站，所有内容不会用来进行牟利，也不会利用任何形式的广告来间接获益，纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。

ICode9

NOI 一轮复习 I：二分图网络流

NOI 一轮复习 I：二分图网络流

阅读须知：

知识清单/目录：

注意事项：

1. 二分图概念与判定

2. 二分图最大匹配

二分图最小点覆盖

二分图最大独立集

二分图最小边覆盖

有向无环图最小路径覆盖

3. 二分图最大权匹配

4. Hall 定理

5. 网络最大流

最大流方案

最小割方案与可行边必经边

二分图最大匹配方案与可行边（点）必经边（点）

6. 最小费用最大流

7. 上下界网络流

无源汇上下界可行流

有源汇上下界可行流

有源汇上下界最大流

有源汇上下界最小流

无源汇上下界最小费用可行流

有源汇上下界最小费用流

有负环的费用流

8. 网络流扩展与建模举例