斜率优化 dp

2020-07-18 16:00:24 阅读：290 来源： 互联网

\(\large斜率优化dp\)

//P2365
#include<cstdio>
#define ll long long
using namespace std;
ll f[5010],sumt[5010],sumc[5010];
int n,s;
ll min(int a,int b){return a<b?a:b;}
signed main(){
 int n,s,t,c;
    scanf("%d%d",&n,&s);
    for (int i=1;i<=n;++i){
        scanf("%d%d",&t,&c);
        sumt[i]=sumt[i-1]+t;
        sumc[i]=sumc[i-1]+c;
    }
    for (int i=1;i<=n;++i)
        f[i]=0x3f3f3f3f;
    for (int i=1;i<=n;++i)
    for (int j=0;j<=i-1;++j)
        f[i]=min(f[i],f[j]+sumc[i]*sumt[i]+s*sumc[n]-sumc[j]*(sumt[i]+s));
    printf("%d",f[n]);
    return 0;
}

\[luoguP2365\\ F[i]=min_{0\le j<i}\{F[j]+sumT[i]*(sumC[i]-sumC[j]+S*(sumC[N]-sumC[j])) \}O(n^2)\\ luoguP5785\\ 数据超级加倍\\ 对上式子进行优化,把常数,仅与i有关的项,仅与j有关的项以及i,j乘积项分离\\ F[i]=min_{0\le j<i}\{ F[j]-(S+sumT[i])*sumC[j]\}+sumT[i]*sumC[i]+S*sumC[N];\\ 去掉min,把关于j的看做变量F[j]和sumC[j],其余部分看做常量\\ 得到F[j]=(S+sumT[i])*sumC[j]+F[i]-sumT[i]*sumC[i]-S*sumC[N];\\ 以sumC[j]为横坐标,F[j]为纵坐标,建立坐标轴,进行线性规划\\ 斜率: sumT(i)+S\\ 纵截距: f(i)−sumT(i)×sumC(i)−S×sumC(n)\\ 我们可以发现纵截距越大,F[i]越大\\ 通俗一点讲，所谓选择最优决策点就是把一条直线从下向上靠，第一个相交的点就是最优决策点（因为此时b最小，f_i也必定最小）。 \]

偷的Chpu437的图 23333

取所有的点,寻找一个凸包(凸多边形)使其围住所有点在凸包上进行线性规划

为了探究最佳决策需要满足的条件, 我们设三个决策为\(j_1,j_2,j_3,且j_1<j_2<j_3\)

从图可以发现,\(j_2\)有可能成为最优结构,当且仅当:

\[\frac{F[j_2]-F[j_1]}{sumC[j_2]-sumC[j_1]}<\frac{F[j_3]-F[j_2]}{sumC[j_3]-sumC[j_2]} \]

在下凸壳,斜率单调递增,下凸壳的顶点才可能成为最优决策,对于某条斜率为k的直线,某顶点左侧线段斜率比k小,

右侧线段比k大,顶点为最优决策,直线斜率满足单调

同时, 由于 sumC 单调递增, 新决策的横坐标一定大于旧决策, 又因为 sumT 单调递增, S+sumT(i), 即 kl 单调递增, 如果我们对于凸壳上每两个相邻顶点的截距, 只保留大于 kl 的部分, 那么最优决策一定在这个凸壳的左端点上.

所以我们建立一个单调队列,若斜率\((F[q[l+1]]-F[q[l]])/(sumC[q[l+1]]-sumC[q[l]])\le S+sumT[i]\)，则把\(q[l]\)出队

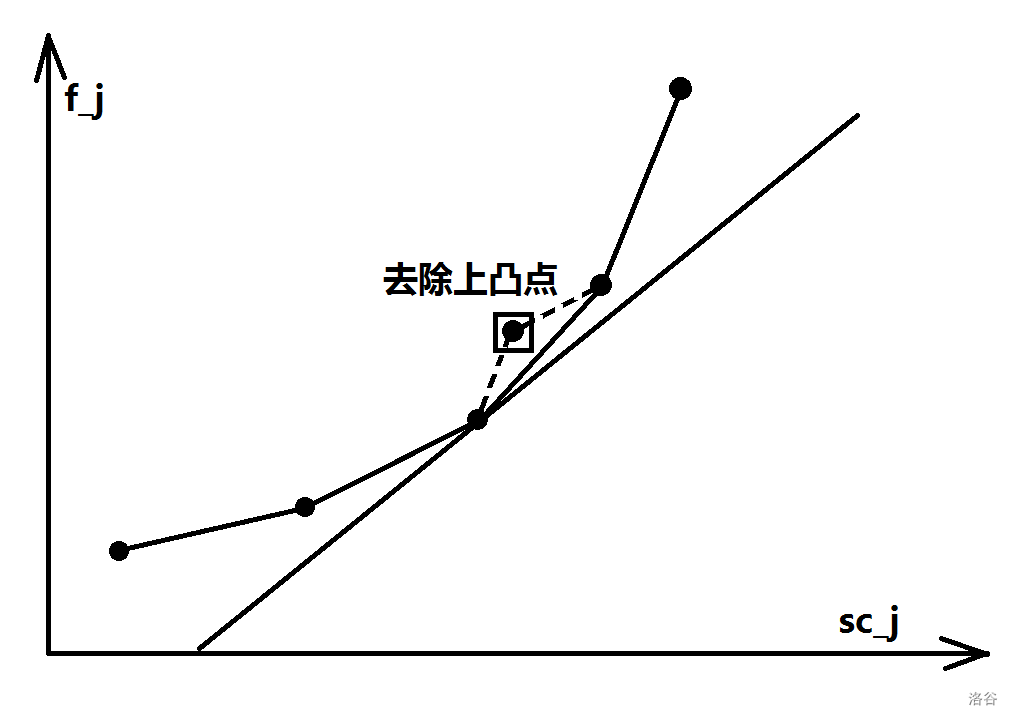
luogu Stay_Hungry 大佬的图

复杂度为O(n)

代码先咕会 咕咕咕

对于斜率为负数时,要找下凸点,维护下凸包

标签：优化,ll,sumT,决策,斜率,dp,sumC,单调
来源： https://www.cnblogs.com/shikeyu/p/13336052.html

本站声明： 1. iCode9 技术分享网（下文简称本站）提供的所有内容，仅供技术学习、探讨和分享；
2. 关于本站的所有留言、评论、转载及引用，纯属内容发起人的个人观点，与本站观点和立场无关；
3. 关于本站的所有言论和文字，纯属内容发起人的个人观点，与本站观点和立场无关；
4. 本站文章均是网友提供，不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属；如您发现该文章侵犯了您的权益，可联系我们第一时间进行删除；
5. 本站为非盈利性的个人网站，所有内容不会用来进行牟利，也不会利用任何形式的广告来间接获益，纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。

ICode9

斜率 优化 dp

斜率优化 dp