标签:总结 剖分 int top 树链 seg 节点 size
目录
一、关于树链剖分
你的好盆友最近抛给你这样一个难题(无中生友):
" 一棵树由n个节点,每个节点都有一个权值w,现在想让你对这棵树完成下列操作:
1.把节点u的权值改为t
2.询问节点u到节点v的权值和
3.节点u到v的最大值 "
你看了看题目,发现这就是树链剖分的板子题...
好吧,那如果你不会树链剖分呢?
...
于是你的朋友告诉你这是树链剖分,并因为你不会树链剖分把你嘲讽了(开玩笑而已啦)...
只观察这个问题的三个操作,你惊讶的发现这是线段树所擅长的事情,即单点修改,区间查询。
实际上,如果这棵树退化成一条链,那么你完全可以用线段树来解决这个问题。
你思考了一下,得出了树链剖分是什么东西:
树链剖分(Query on a Tree)是用来解决维护静态树上路径信息问题的一种数据结构。
现在,机智的你开始考虑如何解决一般形态的树,你发现不论如何修改树的点权,这棵树的形态都不会发生改变。因此只要将一些点链接起来,也就是说把一棵树剖分成若干条链。这样,你维护的路径就变成了几条链,且每一条链都可以作为一个区间,这时你就可以快乐地使用线段树维护了。
树链剖分的难点以及核心也就在这里,如何恰当地将一棵树剖分成若干条“链”。这之后只要将这些作为序列进行维护就可以了。
二、树链剖分实现流程
这里使用的树链剖分方法为轻,重边剖分;
- 轻,重边剖分将树的边分为轻边,重边两种,我们记
size[u]为以u节点为根的子树节点个数,对于任意点u,我们把u的子节点的size值最大的一个节点v叫做“v是u的重儿子”,其中边<u,v>为重边,其余边为轻边。
一棵树的轻边与重边:
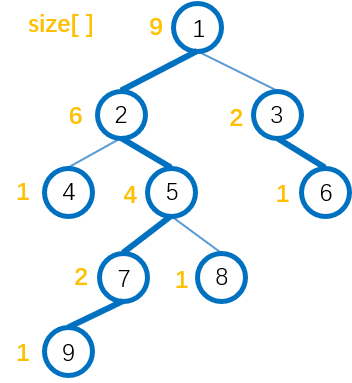
- 当我们发现节点
u的子节点的size[v]大于此时我们已知的重儿子的子树节点数量size[son[u]]时,说明此时son[u]不是最优,那么更改v为重儿子就好了,即if(size[v]>size[son[u]]) son[u]=v;。
特殊地,若节点u的子节点的子树节点个数相等,那么我们把第一个遍历到的子节点作为节点u的重儿子。
轻重边的性质:
1. 若边(u,v)为轻边,那么\(size[v]\leq size[u]/2\)
由于节点u一定有一个重儿子v,节点v的子树大小至少要大于size[u]/2,否则v就不能作为u的重儿子。
2. 从根节点到某一点u的路径中的轻边个数\(\leq O(logn)\)
根据贪心思想,当节点u在叶子节点的时候保证轻边的数量尽量多。由于每经过一条轻边,都会至少减少一半,所以该路径至多有\(O(logn)\)条轻边。
3. 重路径:当一条路径全部由重边组成,那么这个路径为重路径(特殊地,一个点也作为一条重路径)。 有性质:根结点到节点u的路径中,有不超过\(O(logn)\)条轻边和\(O(logn)\)条重路径。
根结点到节点u的轻边个数为\(O(logn)\)条,因此重路径的数量为\(O(logn)\)。
- 当我们对树进行深度优先遍历时,我们优先遍历重儿子,对于重链中的每一个节点
u,始终记录这条重链中深度最小的节点存入top[u]中,其中top数组表示为一条重链中该点能向上跳到的最远节点。
当遍历到递归边界时(!son[u]没有重儿子),我们回溯并开始遍历轻边。遍历到轻边的节点v时,记录top[v]=v。
下图表现了遍历的顺序(包含回溯):
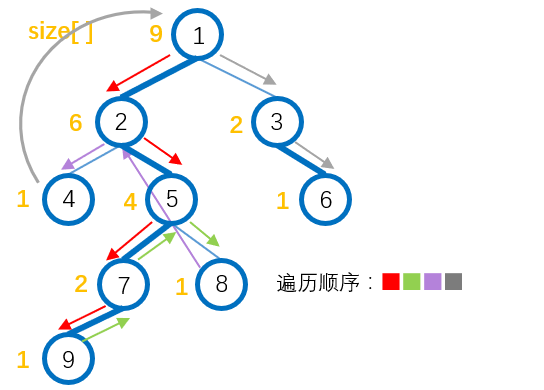
遍历时我们还可以得出每个节点遍历的顺序(DFS序/时间戳),我们把这个顺序记录到seg[ ]数组中,这样就把树上的节点一一映射到序列上了。同时为了我们知道序列上的节点对应树上是哪个节点,我们建立数组rev[ ]记录,即rev[cnt]=u,其中cnt为遍历的顺序。
下图为top,seg数组存储的模拟:
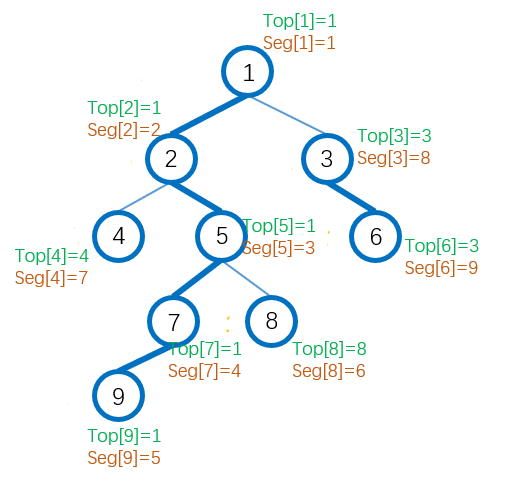
由于我们优先遍历重链,所以我们能保证重链中的节点的DFS序是连续的,这样我们在查询的时候只要线段树查询seg[top[u]]~seg[u]这个区间就可以了。
我们对树进行剖分后,此时维护
<u,v>的路径,我们处理出u,v的最近公共祖先,如果top[x],top[y]不同,那么显然他们的LCA不可能在top深度较大的那条重路径上。
我们优先处理深度较大的一条路径,重边只需要线段树维护,轻边则直接跳过,访问下一个重边。由于拆分重路径的过程就是在求LCA的过程中,我们会选择u,v中深度较深的一点来走,直到u==v,这实际上是暴力思想。
由于我们已经处理出top[ ]数组,我们不需要一步一步向上跳,直接由x跳到fa[top[x]]处。此时由于重链是一个连续的区间,我们可以用线段树进行维护。
当x,y的top相同的时候,说明他们在同一条重路径上,此时的路径也是序列上的区间,且x,y中深度较小的那个点为x,y的最近公共祖先。这样我们就能把任意路径拆分成若干条重路径,转化为区间后就可以用线段树进行处理。
二、树链剖分具体实现
下面结合代码具体分析,以单点修改,区间查询为例
1.需要表示的变量
fa[u]; //节点u的父亲节点,在求LCA时涉及
dep[u]; //节点u的深度,在求LCA时涉及
size[u]; //节点u的子树节点大小,在求重儿子时涉及
son[u]; //节点u的重儿子,在遍历重链以及求dfs序时涉及。
.................
top[u]; //重路径节点u的顶部节点,在求LCA时涉及
seg[u]; //树上节点对应的dfs序,也可以理解为转化到序列上的节点编号,在修改/查询重链时涉及
rev[u]; //dfs序中的编号对应树上的节点编号,或对应的权值,在初始化线段树时涉及2.储存一棵树
采用树图的方式存储,使用链式前向星。
个人比较喜欢使用数组的方式,当然也可以用向量来存。
CodeA:
int first[5000],next[5000],go[5000],tot=0;
inline void add_edge(int u,int v){
next[++tot]=first[u];
first[u]=tot;
go[tot]=v;
}
add_edge(u,v);//主函数内
add_edge(v,u);CodeB:
vector<int> g[5000];
g[u].push_back(v);//主函数内
g[v].push_back(u);3.第一次遍历,处理fa,dep,size,son数组
Code:
比较简洁的写法。
inline void dfs1(int u){
size[u]=1;//子树中只有节点u,因此大小为1
for(int e=frist[u];e;e=next[e]){
int v=go[e];
if(fa[u]==v) continue;//不加会成环
fa[v]=u;//标记v的父亲
dep[v]=dep[u]+1;//计算深度
dfs1(v);
size[u]+=size[v];//回溯的时候累计子树节点大小
if(size[v]>size[son[u]]) son[u]=v; //更新重儿子
}
}
dfs1(1);//主函数内4.第二次遍历,处理top,seg,rev数组
Code:
inline void dfs2(int u,int fath){//这里fath为u的父亲节点
seg[u]=++seg[0];//如果节点序号不涉及0,那么利用一下数组就不用再建变量了
rev[seg[0]]=b[u];//存储dfs序的节点对应树上节点的权值
top[u]=fath;//重儿子所在重链的顶部节点
if(!son[u]) return;//到头了,回溯
dfs2(son[u],fath);//不断遍历重儿子
for(int e=frist[u];e;e=next[e]){//此时遍历轻儿子
int v=go[e];
if(fa[u]==v||v==son[u]) continue;//保证不产生环且不再遍历重儿子
dfs2(v,v);//自己的top是自己
}
}
dfs1(1);//主函数内5.初始化线段树
和一般线段树是一样的。
Code:
inline void push_up(int k){
sumv[k]=sumv[k<<1]+sumv[k<<1|1];
}
inline void build(int k,int l,int r){
if(l==r){
sumv[k]+=rev[l];//sumv记录了线段树的区间和
return;
}
int mid=(l+r)>>1;
build(k<<1,l,mid);
build(k<<1|1,mid+1,r);
push_up(k);//更新,在之后的代码中同理
}
build(1,1,n);//主函数内6.单点修改
和一般线段树也是一样的...
inline void modify_single_point(int k,int l,int r,int pos,int val){
if(l==r){
sumv[k]+=val;
return;
}
mid=(l+r)>>1;
if(pos<=mid) modify_single_point(k<<1,l,mid,pos,val);
else modify_single_point(k<<1|1,mid+1,r,pos,val);
push_up(k);
}
modify_single_point(1,1,n,seg[x],val);//主函数内7.区间修改---以x为根结点的子树内节点的值都加val
seg[ ]数组内保证了dfs序(不懂的话可以对照上面的图模拟一下),因此seg[x]~seg[x]+size[x]-1这一闭区间都是x子树中的节点,接下来就是线段树负责的事了。
Code:
inline void push_down(int k,int l,int r,int mid){
if(lazy[k]==0) reutrn;
lazy[k<<1]+=lazy[k];
lazy[k<<1|1]+=lazy[k];
sumv[k<<1]+=lazy[k]*(mid-l+1);
sumv[k<<1|1]+=lazy[k]*(r-mid);
lazy[k]=0;
}
inline void modify_range(int k,int l,int r,int L,int R,int val){
if(l>=L&&r<=R){
lazy[k]+=val;//延迟标记
sumv[k]+=val*(r-l+1);
return;
}
push_down(k,l,r,mid);//若下文出现push_down,那么同本段代码
int mid=(l+r)>>1;
if(mid>=L) modify_range(k<<1,l,mid,L,R,val);
if(mid<R) modify_range(k<<1|1,mid+1,r,L,R,val);
push_up(k);
}
modify_range(1,1,n,seg[x],seg[x]+size[x]-1,val);//主函数中8.区间修改---节点x到节点y的最短路径中同时加val
求LCA,并更新区间的值。
Code:
inline void solve_as_lca(int x,int y,int val){
while(top[x]!=top[y]){//不相同就一直跳
if(dep[top[x]]<dep[top[y]]) swap(x,y);//先跳top深的
modify_range(1,1,n,seg[top[x]],seg[x],val);//与上一个函数一样
x=fa[top[x]];//更新,跳到重链顶点的父节点上
}
if(dep[x]>dep[y]) swap(x,y);//此时x,y已经在一条重链上,那么区间更新是由深度浅的点到深度深的点
modify_range(1,1,n,seg[x],seg[y],val);
}
solve_as_lca(x,y,val);//主函数内9.区间查询---以x为根结点的子树内节点的值的和
与操作7是一样的,注意要写push_down()。
Code:
inline int query_range(int k,int l,int r,int L,int R){
if(l>=L&&r<=R) return sumv[k];
push_down(k,l,r,mid);
int mid=(l+r)/2,res=0;
if(mid>=L) res+=query_range(k<<1,l,mid,L,R);
if(mid<R) res+=query_range(k<<1|1,mid+1,r,L,R);
return res;
}
query(1,1,n,seg[x],seg[x]+size[x]-1);//主函数中10.区间查询---节点x到节点y的最短路径中节点的和
同样借助LCA的方式,同时累计答案。
Code:
inline int query_as_lca(int x,int y){
int res=0;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
res+=query_range(1,1,n,seg[top[x]],seg[x]);//与操作9的函数是一样的
x=fa[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
res+=query_range(1,1,n,seg[x],seg[y]);
return res;
}
printf("%d",query_as_lca(x,y));//主函数内11.区间查询---节点x到节点y的最短路径中的最大值/最小值
给出最大值的求法,求最小值时将res赋成最大值,其余同最大值求法。
Code:
#define INF 0x3f3f3f3f
inline int query_range_max(int k,int l,int r,int L,int R){
if(l>=L&&r<=R) return maxv[k];
int mid=(l+r)/2,res=-INF;
if(mid>=L) res=max(res,query_range(k<<1,l,mid,L,R));
if(mid<R) res=max(res,query_range(k<<1|1,mid+1,r,L,R));
return res;
}
inline int query_for_max(int x,int y){
int res=-INF;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
res=max(res,query_range_max(1,1,n,seg[top[x]],seg[x]));
x=fa[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
res=max(res,query_range_max(1,1,n,seg[x],seg[y]));
return res;
}
printf("%d",query_for_max(x,y));//主函数内以上就是树链剖分的具体实现以及一些基本操作,
现在你已经可以吊打你的好朋友了(〃'▽'〃)。
三、例题
例1:P3384 【模板】树链剖分
我们所学的操作已经涵盖了题目要求的操作,直接上代码啦(不要忘记取模运算)。
Code:
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1e5+10;
int sumv[N<<2],lazy[N<<2];
int n,q,rt,mod,b[N];
int dep[N],fa[N],seg[N],rev[N],son[N],size[N],top[N];
int first[N<<2],next[N<<1],go[N<<1],tot;
inline void add_edge(int u,int v){
next[++tot]=first[u];
first[u]=tot;
go[tot]=v;
}
inline void dfs1(int u){
size[u]=1;
for(int e=first[u];e;e=next[e]){
int v=go[e];
if(fa[u]==v) continue;
fa[v]=u;dep[v]=dep[u]+1;
dfs1(v);
size[u]+=size[v];
if(size[v]>size[son[u]]) son[u]=v;
}
}
void dfs2(int u,int fath){
seg[u]=++seg[0];
rev[seg[0]]=b[u];
top[u]=fath;
if(!son[u]) return;
dfs2(son[u],fath);
for(int e=first[u];e;e=next[e]){
int v=go[e];
if(v==fa[u]||v==son[u])continue;
dfs2(v,v);
}
}
inline void push_up(int k){sumv[k]=(sumv[k<<1]+sumv[k<<1|1])%mod;}
inline void push_down(int k,int l,int r,int mid){
if(!lazy[k]) return;
lazy[k]%=mod;
lazy[k<<1]+=lazy[k];lazy[k<<1]%=mod;
lazy[k<<1|1]+=lazy[k];lazy[k<<1|1]%=mod;
sumv[k<<1]+=lazy[k]*(mid-l+1);sumv[k<<1]%=mod;
sumv[k<<1|1]+=lazy[k]*(r-mid);sumv[k<<1|1]%=mod;
lazy[k]=0;
}
inline void build(int k,int l,int r){
if(l==r){sumv[k]=rev[l]%mod;return;}
int mid=(l+r)>>1;
build(k<<1,l,mid);
build(k<<1|1,mid+1,r);
push_up(k);
}
inline int query_range(int k,int l,int r,int L,int R){
if(l>=L&&r<=R){return sumv[k]%mod;}
int mid=(l+r)>>1,res=0;//change position
push_down(k,l,r,mid);
if(mid>=L) res+=query_range(k<<1,l,mid,L,R)%mod;res%=mod;
if(mid<R) res+=query_range(k<<1|1,mid+1,r,L,R)%mod;res%=mod;
return res;
}
inline void modify_range(int k,int l,int r,int L,int R,int val){
if(l>=L&&r<=R){
val%=mod;lazy[k]+=val;lazy[k]%=mod;
sumv[k]+=val*(r-l+1);sumv[k]%=mod;
return;
}
int mid=(l+r)>>1;
push_down(k,l,r,mid);
if(mid>=L) modify_range(k<<1,l,mid,L,R,val);
if(mid<R) modify_range(k<<1|1,mid+1,r,L,R,val);
push_up(k);
}
inline int query_as_lca(int x,int y){
int res=0;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
res+=query_range(1,1,n,seg[top[x]],seg[x]);res%=mod;
x=fa[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
res+=query_range(1,1,n,seg[x],seg[y])%mod;res%=mod;
return res;
}
inline void modify_as_lca(int x,int y,int val){
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
modify_range(1,1,n,seg[top[x]],seg[x],val);
x=fa[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
modify_range(1,1,n,seg[x],seg[y],val);
}
int main()
{
scanf("%d%d%d%d",&n,&q,&rt,&mod);
for(int i=1;i<=n;i++) scanf("%d",&b[i]),b[i]%=mod;
for(int i=1,u,v;i<n;i++){
scanf("%d%d",&u,&v);
add_edge(u,v);add_edge(v,u);
}
dfs1(rt);dfs2(rt,rt);
build(1,1,n);
for(int t=1,op,x,y,z;t<=q;t++){
scanf("%d",&op);
if(op==1){
scanf("%d%d%d",&x,&y,&z);
modify_as_lca(x,y,z);
}
else if(op==2){
scanf("%d%d",&x,&y);
printf("%d\n",query_as_lca(x,y));
}
else if(op==3){
scanf("%d%d",&x,&z);
modify_range(1,1,n,seg[x],seg[x]+size[x]-1,z);
}
else if(op==4){
scanf("%d",&x);
printf("%d\n",query_range(1,1,n,seg[x],seg[x]+size[x]-1)%mod);
}
}
return 0;
}其余一些例题:
例2:P2146 [NOI2015]软件包管理器
例3:P2590 [ZJOI2008]树的统计
例4:[JLOI2014]松鼠的新家

标签:总结,剖分,int,top,树链,seg,节点,size 来源: https://www.cnblogs.com/cyanigence-oi/p/11792885.html
本站声明: 1. iCode9 技术分享网(下文简称本站)提供的所有内容,仅供技术学习、探讨和分享; 2. 关于本站的所有留言、评论、转载及引用,纯属内容发起人的个人观点,与本站观点和立场无关; 3. 关于本站的所有言论和文字,纯属内容发起人的个人观点,与本站观点和立场无关; 4. 本站文章均是网友提供,不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属;如您发现该文章侵犯了您的权益,可联系我们第一时间进行删除; 5. 本站为非盈利性的个人网站,所有内容不会用来进行牟利,也不会利用任何形式的广告来间接获益,纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。
