狭义圆方树
任意一条边至多只出现在一条简单回路的无向连通图称为仙人掌。
我们对每一个简单环建一个方点。
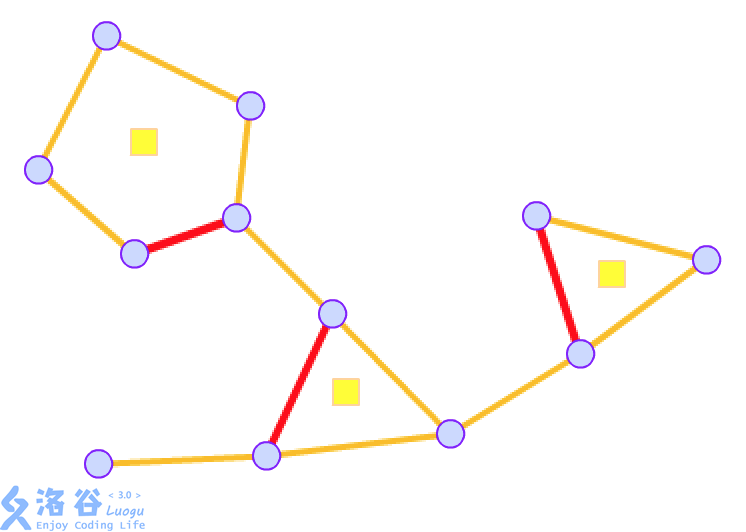
然后这个环上的所有点与这个方点连边,同时删除原先环上的边
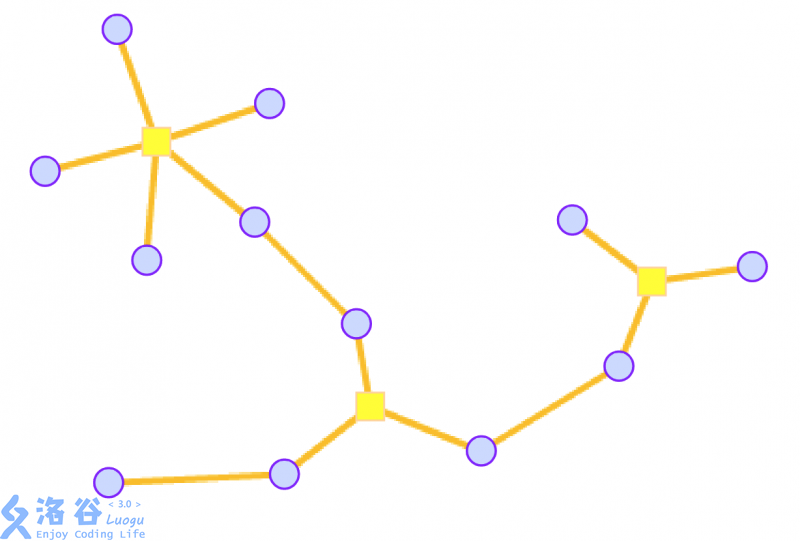
自此我们就建成了一颗狭义圆方树。容易发现不存在相邻的两个方点
P5236 【模板】静态仙人掌
给你一个有 \(n\) 个点和 \(m\) 条边的仙人掌图,和 \(q\) 组询问
每次询问两个点 \(u,v\),求两点之间的最短路。
既然要求得最短路,那么我们还需要确定圆方树上的边的边权。
- 如果 \(u,v\) 都是圆点,权值为原图中边权
- 如果 \(u\) 是方点,\(v\) 是圆点,那么权值为 \(v\) 的 \(u\) 的父亲(即环的顶点)的最短路。
现在询问两点 \(u,v\) 之间的距离,求得 \(u,v\) 的 LCA。
如果 LCA 是圆点,那么答案就是 \(dis_u+dis_v-2\times dis_{lca}\)
如果 LCA 是方点,那么我们需要找到 \(u\) 的在环上的最近祖先节点 \(fu\),和 \(v\) 的在环上的最近祖先 \(fv\),答案就是 \(dis_u-dis_{fu}+dis_v-dis_{fv}\) 加上 \(fu,fv\) 两点在环上的距离。
假设 \(x\) 到环顶点的距离为 \(d(x)\),这个环的总长为 \(len\),那么 \(fu,fv\) 在环上的最短距离就是 \(\min(|d(fu)-d(fv)|,sum-|d(fu)-d(fv)|)\) 。
实现
这玩意的实现难度真的还有点大。
找环可以使用 tarjan 实现,具体如何定位这个环看代码,然后 \(d(x)\) 可以将环拆开来做,求出整个环的长度 \(sum\),然后顺着求到环顶点的距离为 \(dist\),那么 \(d(x)=\min(dist,sum-dist)\)。
求解 \(fu,fv\) 使用倍增的话比较简单,跳 LCA 的时候最后一步不跳就得出来了;使用树剖的话求解需要判断 \(fu\) 是 \(lca\) 的轻儿子或重儿子。如果最后一步跳链顶的父亲跳到了 \(lca\) 这个点,那么 \(fu\) 和 \(lca\) 不在一条重链上,则 \(fu\) 就是那个链顶;反之 \(fu\) 和 \(lca\) 在同一条重链上,\(fu\) 是 \(lca\) 的重儿子。
const int N=100005,M=200005;
struct Edge{
int enxt[M],head[N],to[M],weight[M],ent;
inline void addline(int u,int v,int w){
to[++ent]=v;
weight[ent]=w;
enxt[ent]=head[u];
head[u]=ent;
}
}e1,e2;
int n,m,q;
int low[N],dfn[N],tim,fa[N],liv[N];
int tot,sum[N<<2];
void calc(int u,int v,int val){//u是这个环的起点
++tot;
int tmp=val,loc=v;
while(loc!=fa[u]){
sum[loc]=tmp;
tmp+=liv[loc];
loc=fa[loc];
}
sum[tot+n]=sum[u];
sum[u]=0;//到自己的最短距离为0
loc=v;
while(loc!=fa[u]){
tmp=min(sum[loc],sum[tot+n]-sum[loc]);
e2.addline(tot+n,loc,tmp);
e2.addline(loc,tot+n,tmp);
loc=fa[loc];
}
}
void tarjan(int u,int f){
low[u]=dfn[u]=++tim;
for(int i=e1.head[u];i;i=e1.enxt[i]){
int v=e1.to[i],w=e1.weight[i];
if(!dfn[v]){
fa[v]=u;
liv[v]=w;
tarjan(v,u);
low[u]=min(low[u],low[v]);
}else if(v!=f)
low[u]=min(low[u],dfn[v]);
if(low[v]>dfn[u]){//说明是 圆-圆边
e2.addline(u,v,w),e2.addline(v,u,w);
//printf("yuan2_yuan2 %d %d %d\n",u,v,w);
}
}
for(int i=e1.head[u];i;i=e1.enxt[i]){//找转了一圈回来的点
int v=e1.to[i];
if(fa[v]==u||dfn[v]<=dfn[u])continue;//fa限制了沿着环的第一个点,fa和dfn共同限制了不在一个环内的点
calc(u,v,e1.weight[i]);
}
}
int siz[N],dep[N],dis[N],son[N],fat[N],tps[N];
void dfs1(int u,int f){
fat[u]=f,siz[u]=1,dep[u]=dep[f]+1;
for(int i=e2.head[u];i;i=e2.enxt[i]){
int v=e2.to[i],w=e2.weight[i];
if(v==f)continue;
dis[v]=dis[u]+w;
dfs1(v,u);
siz[u]+=siz[v];
if(siz[v]>siz[son[u]])son[u]=v;
}
}
void dfs2(int u,int t){
tps[u]=t;
if(son[u])dfs2(son[u],t);
for(int i=e2.head[u];i;i=e2.enxt[i]){
int v=e2.to[i];
if(v==fat[u]||v==son[u])continue;
dfs2(v,v);
}
}
inline int __lca(int x,int y){
while(tps[x]!=tps[y]){
if(dep[tps[x]]<dep[tps[y]])swap(x,y);
x=fat[tps[x]];
}return dep[x]<dep[y]?x:y;
}
inline int findson(int x,int tar){
int loc=0;
while(tps[x]!=tps[tar]){
loc=tps[x];
x=fat[tps[x]];
}if(x==tar)return loc;//是轻儿子
else return son[tar];//是重儿子
}
int main(){
n=read(),m=read(),q=read();
for(int i=1;i<=m;++i){
int u=read(),v=read(),w=read();
e1.addline(u,v,w);e1.addline(v,u,w);
}
tarjan(1,0);
// for(int i=1;i<=n;++i){
// printf("%d %d %d %d %d\n",i,dfn[i],low[i],fa[i],liv[i]);
// }
dfs1(1,0);dfs2(1,1);//树剖
for(int i=1;i<=q;++i){
int x=read(),y=read(),lca=__lca(x,y),ans=0;
if(lca<=n)ans=dis[x]+dis[y]-2*dis[lca];//lca是圆点
else{
int belx=findson(x,lca),bely=findson(y,lca),der=abs(sum[belx]-sum[bely]);
ans=dis[x]-dis[belx]+dis[y]-dis[bely]+min(der,sum[lca]-der);
}
printf("%d\n",ans);
}
return 0;
}
广义圆方树
正片开始
狭义圆方树是对每一个简单环建一个方点,而广义圆方树是对每个点双连通分量建一个方点。

int dfn[N],low[N],tim,stk[N],top;
void tarjan(int u){
dfn[u]=low[u]=++tim;
stk[++top]=u;
for(int i=e1.head[u];i;i=e1.enxt[i]){
int v=e1.to[i];
if(!dfn[v]){
tarjan(v);
low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u]){
e2.addedge(++tot,u);
int x=0;
do{
x=stk[top--];
e2.addedge(tot,x);
}while(x!=v);
}
}else low[u]=min(low[u],dfn[v]);
}
}
e2 就是我们建出来的圆方树。
基本性质
- 一个圆点必然只和方点相连,一个方点必然只和圆点相连
例题
P4320 道路相遇
给定一张 \(n\) 个点 \(m\) 条边的无向连通图,给定 \(q\) 个询问 \(u,v\),求出 \(u\) 到 \(v\) 路径之间必须经过的点。
一个显然的结论是在一个割点两侧的点想要互相到达必须经过这个割点。
那么 \(u\) 到 \(v\) 之间必经点的个数就是他们之间的割点数,同时这两个点本身也必须被经过。所以答案就是圆方树树上两点之间的圆点个数。
然后因为路径上的点一定是圆点方点交接的,所以假如路径的长度为 \(len\),那么圆点的个数就是 \(len/2+1\) 个。
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
inline int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||'9'<ch){if(ch=='-')f=-1;ch=getchar();}
while('0'<=ch&&ch<='9'){x=x*10+(ch^48);ch=getchar();}
return x*f;
}
const int N=1000006,M=4000006;
struct Edge{
int enxt[M],head[N],to[M],ent;
inline void addline(int u,int v){
to[++ent]=v;
enxt[ent]=head[u];
head[u]=ent;
}
inline void addedge(int u,int v){
//printf("addedge %d %d\n",u,v);
addline(u,v);
addline(v,u);
}
}e1,e2;
int n,m,tot;
int dfn[N],low[N],tim,stk[N],top;
void tarjan(int u){
dfn[u]=low[u]=++tim;
stk[++top]=u;
for(int i=e1.head[u];i;i=e1.enxt[i]){
int v=e1.to[i];
if(!dfn[v]){
tarjan(v);
low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u]){//点双
e2.addedge(++tot,u);
int x=0;
do{
x=stk[top--];
e2.addedge(tot,x);
}while(x!=v);
}
}else low[u]=min(low[u],dfn[v]);
}
}
int siz[N],dep[N],son[N],tps[N],fat[N];
void dfs1(int u,int f){
siz[u]=1,fat[u]=f,dep[u]=dep[f]+1;
for(int i=e2.head[u];i;i=e2.enxt[i]){
int v=e2.to[i];
if(v==f)continue;
dfs1(v,u);
siz[u]+=siz[v];
if(siz[v]>siz[son[u]])son[u]=v;
}
}
void dfs2(int u,int t){
tps[u]=t;
if(son[u])dfs2(son[u],t);
for(int i=e2.head[u];i;i=e2.enxt[i]){
int v=e2.to[i];
if(v==fat[u]||v==son[u])continue;
dfs2(v,v);
}
}
inline int __lca(int x,int y){
while(tps[x]!=tps[y]){
if(dep[tps[x]]<dep[tps[y]])swap(x,y);
x=fat[tps[x]];
}return dep[x]<dep[y]?x:y;
}
int main(){
tot=n=read(),m=read();
for(int i=1;i<=m;++i){
int u=read(),v=read();
e1.addedge(u,v);
}
tarjan(1);
dfs1(1,0);dfs2(1,1);
int q=read();
while(q--){
int u=read(),v=read(),lca=__lca(u,v);
printf("%d\n",(dep[u]+dep[v]-2*dep[lca])/2+1);
}
return 0;
}
UVA1464 Traffic Real Time Query System
一个城市有 \(n\) 个路口,\(m\) 条无向公路。求从第 \(S\) 条路到第 \(T\) 条路必须经过的点有几个。
结论:只需要将这两个边4个点任意两两求一遍路径中的圆点数(不包含两端点),最后取最大值即可。
如果一条边的两个端点均非割点,那么求出来的路径答案是一样的。如果一条边的两个端点均是割点或者一个是割点一个不是割点,那么路径中的必经点显然包含其中的一个割点,那么我们取最大值的时候这个要求的割点就会算在里面。
整体代码与 LG4320 相同,注意多组数据,贴一个部分代码。
inline int solve(int x,int y){
int lca=__lca(x,y);
return (dep[x]+dep[y]-2*dep[lca])/2-1;
}
int main(){
int T=read();
while(T--){
//prework
while(q--){
int x=read(),y=read();
printf("%d\n",max(max(solve(uu[x],uu[y]),solve(vv[x],vv[y])),max(solve(uu[x],vv[y]),solve(vv[x],uu[y]))));
}
}
}
CF487E Tourists
给定一张 \(n\) 个点 \(m\) 条边的无向连通图,每个点有一个值 \(w_i\)。现在给出 \(q\) 个共两种操作
C a w,将 \(a\) 点的值变为 \(w\)。A a b,询问 \(a\) 到 \(b\) 的路径中的最小值。
先建出圆方树。圆方树上的每个方点上挂一个 multiset,维护这个方点所管辖的所有点的权值。
对于每次修改操作,修改的必然是圆点,为了保证复杂度正确,我们不必修改每个与这个圆点相邻的方点的 multiset,而是只用修改这个圆点的父亲方点的 multiset。所以对于查询的操作,我们不仅要求得路径上每个圆点或方点的最大值,如果路径两端点的 \(lca\) 是方点,那么还需要查询这个方点的父亲的值。
至于如何求路径最大值和 \(lca\),树剖一下线段树维护就好了。
multiset<int>se[N];
int n,m,q,tot;
int low[N],dfn[N],tim,stk[N],top,col[N];
void tarjan(int u){
low[u]=dfn[u]=++tim;
stk[++top]=u;
for(int i=e1.head[u];i;i=e1.enxt[i]){
int v=e1.to[i];
if(!dfn[v]){
tarjan(v);
low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u]){
e2.addedge(++tot,u);
int x=0;
do{
x=stk[top--];//这里面的x不要再用int定义了
e2.addedge(x,tot);
}while(x!=v);
}
}else low[u]=min(low[u],dfn[v]);
}
}
int siz[N],fat[N],son[N],dep[N],tps[N],lis[N],val[N];
void dfs1(int u,int f){
siz[u]=1,fat[u]=f,dep[u]=dep[f]+1;
for(int i=e2.head[u];i;i=e2.enxt[i]){
int v=e2.to[i];
if(v==f)continue;
dfs1(v,u);
siz[u]+=siz[v];
if(siz[v]>siz[son[u]])son[u]=v;
}
}
void dfs2(int u,int t){
tps[u]=t;dfn[u]=++tim;lis[tim]=u;
if(son[u])dfs2(son[u],t);
for(int i=e2.head[u];i;i=e2.enxt[i]){
int v=e2.to[i];
if(v==fat[u]||v==son[u])continue;
dfs2(v,v);
}
}
struct segtree{
int left,right,minv;
}t[N<<2];
#define ls p<<1
#define rs p<<1|1
inline void pushup(int p){t[p].minv=min(t[ls].minv,t[rs].minv);}
void buildtree(int p,int l,int r){
t[p].left=l,t[p].right=r;
if(l==r){t[p].minv=val[lis[l]];return;}
int mid=(l+r)>>1;
buildtree(ls,l,mid);buildtree(rs,mid+1,r);
pushup(p);
}
void update(int p,int l,int v){
if(t[p].left==t[p].right){
t[p].minv=v;
return;
}
if(l<=t[ls].right)update(ls,l,v);
else update(rs,l,v);
pushup(p);
}
int query(int p,int l,int r){
if(l<=t[p].left&&t[p].right<=r)
return t[p].minv;
int tmp=INF;
if(l<=t[ls].right)tmp=min(tmp,query(ls,l,r));
if(r>=t[rs].left)tmp=min(tmp,query(rs,l,r));
return tmp;
}
inline int minvline(int x,int y){
int tmp=INF;
while(tps[x]!=tps[y]){
if(dep[tps[x]]<dep[tps[y]])swap(x,y);
tmp=min(tmp,query(1,dfn[tps[x]],dfn[x]));
x=fat[tps[x]];
}if(dep[x]>dep[y])swap(x,y);
tmp=min(tmp,query(1,dfn[x],dfn[y]));
if(x>n)tmp=min(tmp,val[fat[x]]);
return tmp;
}
int main(){
tot=n=read(),m=read(),q=read();
for(int i=1;i<=n;++i)
val[i]=read();
for(int i=1;i<=m;++i){
int u=read(),v=read();
e1.addedge(u,v);
}
for(int i=1;i<=n;++i)
if(!dfn[i])tarjan(i);
tim=0;
dfs1(1,0);dfs2(1,1);
for(int i=2;i<=n;++i)
se[fat[i]-n].insert(val[i]);
for(int i=n+1;i<=tot;++i)
val[i]=se[i-n].empty()?INF:*se[i-n].begin();
buildtree(1,1,tot);
while(q--){
char opt[2];int u,v;
scanf("%s",opt);u=read(),v=read();
if(opt[0]=='C'){
update(1,dfn[u],v);
int tmp=val[u];val[u]=v;//这里要把先前的val[u]存起来方便修改
if(u==1)continue;//不用考虑方点,因为没有祖先
int x=fat[u];//方点
se[x-n].erase(se[x-n].find(tmp));
se[x-n].insert(v);
int minv=*se[x-n].begin();
if(minv!=val[x]){
val[x]=minv;
update(1,dfn[x],minv);
}
}else printf("%d\n",minvline(u,v));
}
return 0;
}
P4630 [APIO2018] 铁人两项
给出一张无向图,问存在多少组 \((s,c,f)\),使得 \(s\) 可以经过 \(c\) 到达 \(f\)。
首先思考一颗树的计算方式,显然可以树形 \(dp\) 来做,代码:
void dfsp(int u,int f){
for(auto v:tree[u]){
if(v==f)continue;
dfsp(v,u);ans+=siz[v]*siz[u];
siz[u]+=siz[v];
}
siz[u]+=1ll;
ans+=(all-siz[u])*(siz[u]-1);//可能是森林,所以用all记录总的大小
}
如果是一张图的话,我们从圆方树的角度思考这个问题。首先只对圆点统计 \(size\),对于方点,我们只是方便计数,并不是一个具体存在的点。对于圆点,我们的转移和一颗树的情况相同。对于方点,我们要特别考虑。
假设 \(bas\) 为方点所代表的点双的大小,如果 \(s,f\) 都在方点所代表的点双内,显然中转点有 \(bas-2\) 个;如果 \(s,f\) 均不在点双中,那么有 \(bas\) 个中转点,然而 \(2\) 个圆点会已经计算过一次,所以有 \(bas-2\) 个中转点,如果 \(s\) 和 \(f\) 有且只有一个在方点所在的环中,那么会有 \(bas-1\) 个中转点,然而会有一个在方点外的点被多算一次,所以还是 \(bas-2\) 个中转点。
所以方点在计算的时候乘上一个 \(bas-2\) 的系数。
const int N=400005;
int n,m,all,tot;
vector<int>edge[N],tree[N];
int dfn[N],low[N],stk[N],top,tim,num;
void tarjan(int u,int f){
dfn[u]=low[u]=++tim;++all;
stk[++top]=u;
for(auto v:edge[u]){
if(v==f)continue;
if(!dfn[v]){
tarjan(v,u);
low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u]){
tree[++tot].push_back(u);
tree[u].push_back(tot);
int x=0;
do{
x=stk[top--];
tree[tot].push_back(x);
tree[x].push_back(tot);
}while(x!=v);
}
}else low[u]=min(low[u],dfn[v]);
}
}
ll siz[N],ans;
void dfsp(int u,int f){
ll num=tree[u].size();
for(auto v:tree[u]){
if(v==f)continue;
dfsp(v,u);
if(u<=n)ans+=siz[v]*siz[u];
else ans+=siz[v]*siz[u]*(num-2);
siz[u]+=siz[v];
}
if(u<=n){
siz[u]+=1ll;//为了方便统计答案,siz在这里更新(是+=)
ans+=(all-siz[u])*(siz[u]-1);
}else ans+=(all-siz[u])*siz[u]*(num-2);
}
int main(){
tot=n=read(),m=read();
for(int i=1;i<=m;++i){
int u=read(),v=read();
edge[u].push_back(v);
edge[v].push_back(u);
}
for(int i=1;i<=n;++i){
if(!dfn[i]){
all=0;
tarjan(i,i);
dfsp(i,0);
}
}
printf("%lld\n",ans*2);
return 0;
}
P4606 [SDOI2018]战略游戏
省选临近,放飞自我的小 \(Q\) 无心刷题,于是怂恿小 \(C\) 和他一起颓废,玩起了一款战略游戏。
这款战略游戏的地图由 \(n\) 个城市以及 \(m\) 条连接这些城市的双向道路构成,并且从任意一个城市出发总能沿着道路走到任意其他城市。
现在小 \(C\) 已经占领了其中至少两个城市,小 \(Q\) 可以摧毁一个小 \(C\) 没占领的城市,同时摧毁所有连接这个城市的道路。只要在摧毁这个城市之后能够找到某两个小 \(C\) 占领的城市 \(u\) 和 \(v\),使得从 \(u\) 出发沿着道路无论如何都不能走到 \(v\),那么小 \(Q\) 就能赢下这一局游戏。
小 \(Q\) 和小 \(C\) 一共进行了 \(q\) 局游戏,每一局游戏会给出小 \(C\) 占领的城市集合 \(S\),你需要帮小 \(Q\) 数出有多少个城市在他摧毁之后能够让他赢下这一局游戏。
不管怎么说先建个圆方树再说(
sol.1
一个暴力的想法是枚举一对给定的点,求他们路径上的非叶节点的圆点,这些点的并集为答案。这样复杂度 \(O(s^2)\)。
实际上是要求:在圆方树中,包含所有给出的点的联通块,最小的大小,再减去 \(s\) 即为答案。
发现,如果这些点按照 dfs 序排序之后,按照顺序走所有点,再从第 \(s\) 个点走回第 \(1\) 个点。在走过的路径中,如果不考虑相邻两个点的 LCA,每个点恰好被走过两次,这些走过的点恰好就是我们要求的联通块。最后我们会发现第一个点和第 \(s\) 个的 \(lca\) 不会被统计到,加上就好了。同时要减去这 \(s\) 个点本身。
sol.2
看起来就像虚树的样子。我们建出建出圆方树之后对这些建一颗虚树。
可以发现虚树上所有不是询问本身的点的圆点都是合法的。那么我们只需要使用一个树形 DP 统计虚树上的满足条件的点即可。
我们首先需要一次 dfs 求出所有点到根节点(人为定义的)之间的圆点的个数 \(sum\)。
然后树形 dp 的时候记录每个点的子树中所包含的询问点的个数 \(siz\),如果一个点 \(s-siz>0,siz>0\),那么说明这个点删掉之后会有至少一对点不连通,那么就统计这个点的答案,如果这个点本身是询问点,就是 \(sum[f_1]-sum[f_2]\),其中 \(f_2\) 是虚树中的父亲节点, \(f_1\) 是原树的父亲节点;如果不是询问点,就是 \(sum[u]-sum[f2]\)。
同时,如果一个点不满足上述条件,但是他有至少儿子节点的 \(siz>0\),并且他不是询问点,自然这个点也满足条件。
其实具体见代码就好了。
int dfn[N],low[N],stk[N],top,tim,cut[N];
void tarjan(int u,int f){
int num=0;
dfn[u]=low[u]=++tim;
stk[++top]=u;
for(int i=e.head[u];i;i=e.enxt[i]){
int v=e.to[i];
if(!dfn[v]){
tarjan(v,u);
low[u]=min(low[u],low[v]);
if(u==f)++num;
if(low[v]>=dfn[u]){
cut[u]=1;
t.addedge(++tot,u);
int x=0;
do{
x=stk[top--];
t.addedge(tot,x);
}while(x!=v);
}
}else low[u]=min(low[u],dfn[v]);
}
if(u==f&&num>=2)cut[u]=1;
}
int dep[N],fa[N][22],sum[N];
void dfs(int u,int f){
fa[u][0]=f,dep[u]=dep[f]+1,sum[u]=sum[f]+cut[u];dfn[u]=++tim;
for(int i=t.head[u];i;i=t.enxt[i]){
int v=t.to[i];
if(v==f)continue;
dfs(v,u);
}
}
inline int qrlca(int x,int y){
if(dep[x]<dep[y])swap(x,y);
int der=dep[x]-dep[y];
for(int i=20;i>=0;--i)
if((der>>i)&1)x=fa[x][i];
if(x==y)return x;
for(int i=20;i>=0;--i)
if(fa[x][i]!=fa[y][i])
x=fa[x][i],y=fa[y][i];
return fa[x][0];
}
inline bool cmp(int x,int y){return dfn[x]<dfn[y];}
void pushstk(int u){
if(u==1)return;
int lca=qrlca(u,stk[top]);
if(lca!=stk[top]){
while(dfn[lca]<dfn[stk[top-1]])
e.addedge(stk[top-1],stk[top]),--top;
if(lca!=stk[top-1]){
e.head[lca]=0;
e.addedge(lca,stk[top]);
stk[top]=lca;
}else e.addedge(lca,stk[top--]);
}
e.head[u]=0;stk[++top]=u;
}
void buildit(){
e.ent=0;e.head[1]=0;stk[top=1]=1;//此时e存虚树
sort(lis+1,lis+1+k,cmp);
for(int i=1;i<=k;++i)pushstk(lis[i]);
for(int i=1;i<top;++i)e.addedge(stk[i],stk[i+1]);
}
int siz[N];
void dfsp(int u,int f){
int cnt=0;
siz[u]=isk[u];
for(int i=e.head[u];i;i=e.enxt[i]){
int v=e.to[i];
if(v==f)continue;
dfsp(v,u);//这里写成dfs了,我去,还是通过dfn查出来的
if(siz[v])++cnt;
siz[u]+=siz[v];
}
if(k-siz[u]&&siz[u]){
if(isk[u]){
ans+=max(sum[fa[u][0]]-sum[f],0);//这个点是关键点,不能算,取他在原树上的父亲节点。
}
else{
ans+=sum[u]-sum[f];//x到f中的所有点割点均合法,注意这里是[x,f)
}
}else //这里是else 关系!
if(cnt>=2&&!isk[u]){
ans+=(u<=n);//这个点就必须是原树上的点了
}
}
int main(){
int T=read();
while(T--){
tot=n=read(),m=read();
e.init();
for(int i=1;i<=m;++i){
int u=read(),v=read();
e.addedge(u,v);
}
t.init();
memset(dfn,0,sizeof(dfn));tim=top=0;
memset(cut,0,sizeof(cut));//没有清空这个
tarjan(1,1);
memset(dfn,0,sizeof(dfn));tim=0;//此时为树的dfn序
dfs(1,0);
for(int i=1;i<=20;++i)//忘记处理这个了。。。
for(int j=1;j<=tot;++j)
fa[j][i]=fa[fa[j][i-1]][i-1];
int q=read();
while(q--){
k=read();ans=0;//破案了,这里之前写的int k=read(),没赋到全局变量里面
for(int i=1;i<=k;++i)
isk[lis[i]=read()]=1;
buildit();
dfsp(1,0);
printf("%d\n",ans);
for(int i=1;i<=k;++i)
isk[lis[i]]=0;
}
}
return 0;
}
标签:int,siz,方点,dfn,low,圆方树,e2 来源: https://www.cnblogs.com/BigSmall-En/p/16627180.html
本站声明: 1. iCode9 技术分享网(下文简称本站)提供的所有内容,仅供技术学习、探讨和分享; 2. 关于本站的所有留言、评论、转载及引用,纯属内容发起人的个人观点,与本站观点和立场无关; 3. 关于本站的所有言论和文字,纯属内容发起人的个人观点,与本站观点和立场无关; 4. 本站文章均是网友提供,不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属;如您发现该文章侵犯了您的权益,可联系我们第一时间进行删除; 5. 本站为非盈利性的个人网站,所有内容不会用来进行牟利,也不会利用任何形式的广告来间接获益,纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。
