标签：insert int 矩阵 差分 798 数组 include AcWing

二维差分

我们已经知道了一维差分如何去做，那么如果扩展到二维呢？这里就要引入二维差分了。

定义

给定一个数组 \(a\)，构造一个数组 \(b\)，使得 \(a\) 数组是 \(b\) 数组的前缀和数组，那么称 \(b\) 数组是 \(a\) 数组的差分数组。

作用

在 \(O(1)\) 的复杂度内将原矩阵中的任意子矩阵的每个数加上 \(c\)（减法相同）。

具体实现 & 原理

如何构造差分数组？

我们先来考虑如何在 在 \(O(1)\) 的复杂度内将原矩阵中的任意子矩阵的每个数加上/减去 \(c\)。

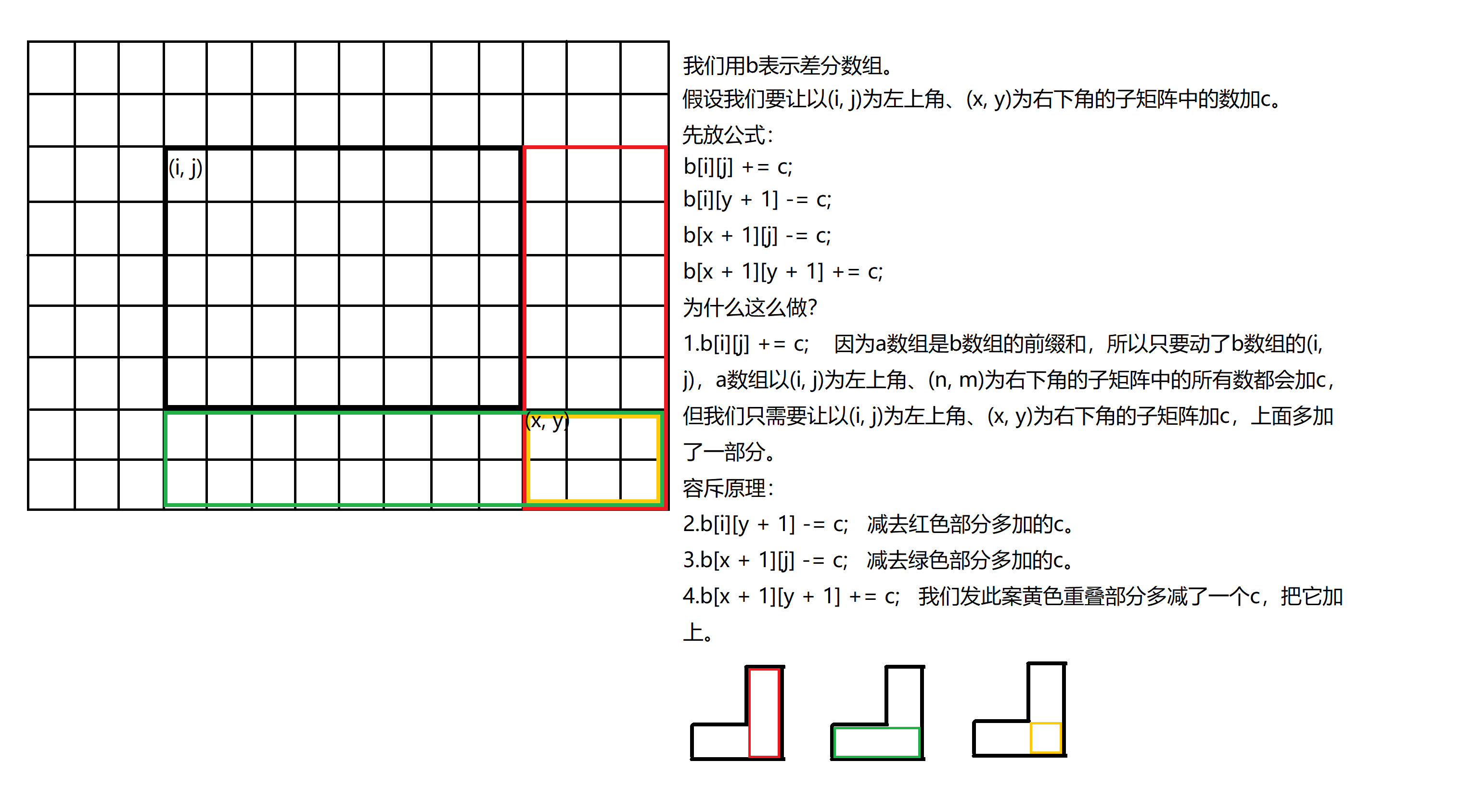
将上述操作封装成函数形式：

void insert(int i, int j, int x, int y, int c)
{
    b[i][j] += c;
    b[i][y + 1] -= c;
    b[x + 1][j] -= c;;
    b[x + 1][y + 1] += c;
}

我们可以让 \(a\) 数组初始时为空，那么显然 \(b\) 数组也为空。

假设 \(a_{i, j}\) 这个格子里的数为 \(c\)，怎么把它加上呢？

可以将左上角 \((i, j)\)、右下角 \((i, j)\) 的子矩形加上 \(c\)（其实就是把 \((i, j)\) 这个小方格加上 \(c\)）。

上述操作代码如下

// 将a[i][j]这个格子赋值为c
insert(i, j, i, j, c);

同理，以为差分也可以这样做，这里不再赘述，详见一维差分。

完整代码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <cmath>
using namespace std;

const int N = 1010;

int a[N][N], b[N][N];

void insert(int i, int j, int x, int y, int c)
{
    b[i][j] += c;
    b[i][y + 1] -= c;
    b[x + 1][j] -= c;;
    b[x + 1][y + 1] += c;
}

int main()
{
    int n, m, q, x, y, xx, yy, c;
    scanf("%d%d%d", &n, &m, &q);
    for (int i = 1; i <= n; i ++ )
    {
        for (int j = 1; j <= m; j ++ )
        {
            scanf("%d", &a[i][j]);
        }
    }
    // 初始化差分矩阵
    for (int i = 1; i <= n; i ++ )
    {
        for (int j = 1; j <= m; j ++ )
        {
            insert(i, j, i, j, a[i][j]);
        }
    }
    for (int i = 0; i < q; i ++ )
    {
        scanf("%d%d%d%d%d", &x, &y, &xx, &yy, &c);
        insert(x, y, xx, yy, c); // 处理每个操作
    }
    for (int i = 1; i <= n; i ++ )
    {
        for (int j = 1; j <= m; j ++ )
        {
            b[i][j] += b[i][j - 1] + b[i - 1][j] - b[i - 1][j - 1]; // 二维前缀和，详见https://www.cnblogs.com/FXT1110011010OI/p/16549503.html
        }
    }
    for (int i = 1; i <= n; i ++ )
    {
        for (int j = 1; j <= m; j ++ )
        {
            printf("%d ", b[i][j]);
        }
        printf("\n");
    }
    return 0;
}

标签：insert,int,矩阵,差分,798,数组,include,AcWing
来源： https://www.cnblogs.com/FXT1110011010OI/p/16573774.html

本站声明： 1. iCode9 技术分享网（下文简称本站）提供的所有内容，仅供技术学习、探讨和分享；
2. 关于本站的所有留言、评论、转载及引用，纯属内容发起人的个人观点，与本站观点和立场无关；
3. 关于本站的所有言论和文字，纯属内容发起人的个人观点，与本站观点和立场无关；
4. 本站文章均是网友提供，不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属；如您发现该文章侵犯了您的权益，可联系我们第一时间进行删除；
5. 本站为非盈利性的个人网站，所有内容不会用来进行牟利，也不会利用任何形式的广告来间接获益，纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。