无损加密
题目描述
\(n\times m\) 的矩形,进行 \(q\) 次变换,设 \(k\) 次变换后的矩阵是 \(A_k\),初始 \(A_0\) 是单位矩阵。每次变换给定 \((l_k,r_k,c_k,d_k)\):
\[(A_k)_{ij}=\begin{cases}d_k(A_{k-1})_{ij} & j\not\in [l_k,r_k]\\d_k\sum_{t=l_k}^j(c_k)^{j-t}(A_{k-1})_{it} & j\in[l_k,r_k]\\\end{cases} \]求 \(f(A_q)\),其中 \(f(B)\) 定义为:
\[f(B)=\Big(\sum_{S\subseteq\{1,2...m\},|S|=n}\det B_{S}\Big)\bmod (10^9+7) \]其中 \(B_S\) 表示矩阵 \(B\) 的所有行与 \(S\) 中元素对应的列,交叉处生成的一个 \(n\times |S|\) 的矩阵。
数据范围保证对于所有的 \(1\leq i\leq m\),都有:
\[\sum_{i=1}^q[i\in[l_k,r_k]]\leq s \]\(2\leq n\leq m\leq 2\cdot 10^5,1\leq s\leq 8,q\leq sm\)
解法
真理:永远不要丝门弄数。
这题没有什么好的突破口,考虑从答案的角度入手,我们如何理解答案中出现的行列式?
谈到行列式,丝告诉我们,常见的模型有:\(\tt Binet-Cauthy\) 公式、矩阵树定理、\(\tt LGV\) 引理。最和本题贴合的是 \(\tt LGV\) 引理,我们把矩阵理解成 \(\tt LGV\) 引理中两点间路径的方案数,考虑构造一张分层图:
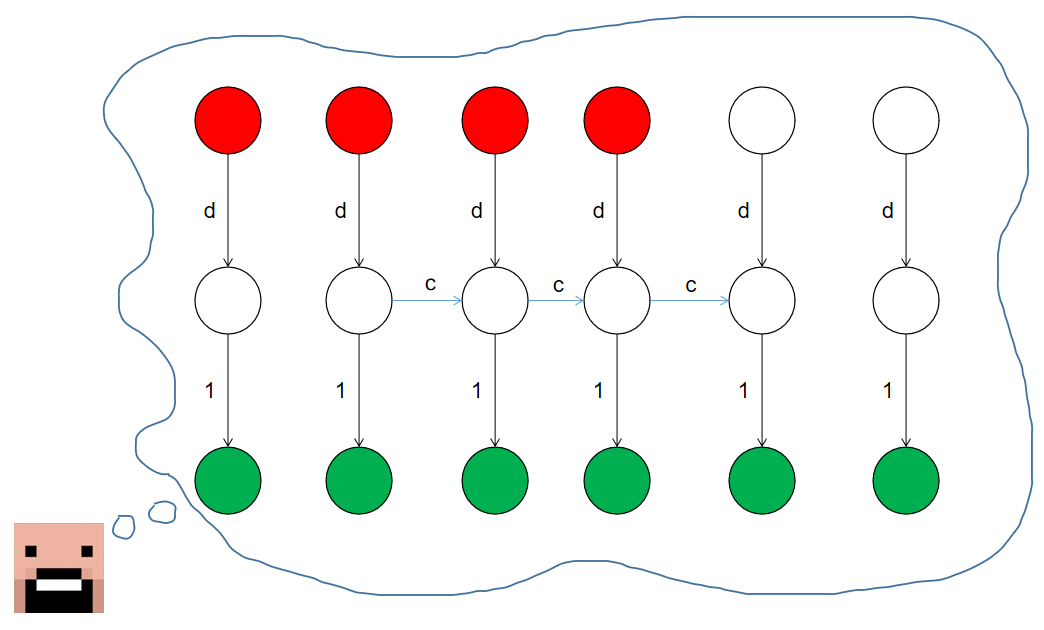
解释一下上面的构造:第一层有 \(n\) 个红点代表起点;最后一层有 \(m\) 个绿点代表终点。根据 \(\tt LGV\) 引理,我们只需要求出 \(n\) 条点不相交的路径,从红点开始在绿点结束的方案数。路径的权值是边权的乘积,方案的权值是路径权值的乘积。
再解释一下 \(B_S\) 这个东西,这对应了方案中的任意选择终点,所以被考虑进去了。
每一次变换相当于添加了 \(m\) 个点,和上一层的对应点连一条边权为 \(d\) 的边。对于在 \([l_i,r_i)\) 中的点,和下一个点连一条边权为 \(c\) 的边,这样构造正好能对应变换规则。
那么问题转化成在上图中求 \(n\) 条不交路径的方案数,直接 \(dp\) 很困难。
利用题目中 \(s\) 的条件,考虑切换 \(dp\) 主体,即我们不再按行 \(dp\) 而是按列 \(dp\)。那么每一列最多存在 \(9\) 个路径暂时的终点,可以暴力状压下来,设 \(dp[i][s]\) 表示考虑到第 \(i\) 列,集合 \(s\) 中的点作为终点的方案数(全集是这一列所有存在入边的点)
一个暴力的转移方法是,我们枚举这一层每个点对应走到下一层的哪个点,由于不交的限制,复杂度大概是 \(O(q\cdot 2^{2s})\)
再深入的分析,其实每个点都对应着下一层的一个范围,这个范围中的点是只有这个点能走到的。所以可以先传递给下一层离得最近的一个点,再考虑到下一层的时候考虑层间的转移,复杂度大概是 \(O(q\cdot 2^{s})\)
对于前 \(i\leq n\) 列,转移时需要加入起点;如果终点在 \(s\) 中,转移到下一层时需要把终点删除(代表这条路径结束)
还是不太好讲清楚,可以结合代码理解具体怎么 \(dp\) 的。
真理:永远不要丝门弄数。
总结
这种逆向思考的题目通常是难以下手的,但是出题人造出这道题一定是正向出发的。
所以正确的打开方式是,抓住题目中有特征的关键东西,然后考虑和这东西有关的理论,尝试套用一些经典模型。
#pragma GCC optimize("Ofast")
#pragma GCC target("avx", "sse")
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
using namespace std;
const int M = 200005;
#define int long long
#define pb push_back
#define z(x) (1<<(x))
const int MOD = 1e9+7;
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,k,po,dp[2][1<<9];vector<int> v[M],W[M];
int qkpow(int a,int b)
{
int r=1;
while(b>0)
{
if(b&1) r=r*a%MOD;
a=a*a%MOD;
b>>=1;
}
return r;
}
void add(int &x,int y) {x=(x+y)%MOD;}
signed main()
{
freopen("encode.in","r",stdin);
freopen("encode.out","w",stdout);
n=read();m=read();k=read();po=1;
for(int cnt=0;k--;)
{
int l=read(),r=read(),c=read(),h=read();
po=po*h%MOD;
for(int i=l;i<r;i++)
v[i].pb(++cnt),W[i].pb(c);
}
dp[0][0]=1;
for(int t=1,w=0;t<=m+1;t++,w^=1)
{
memset(dp[w^1],0,sizeof dp[w^1]);
static int a[11]={},b[11]={},d[11]={};
int n1=0,n2=0;
for(auto x:v[t-1]) a[n1++]=x;
for(auto x:v[t]) b[n2++]=x;
for(int i=0,k=0;i<n1;i++)
{
while(k<n2 && b[k]<a[i]) k++;
d[i]=k;
}
//down
for(int i=0;i<n1;i++)
for(int s=0;s<z(n1+1);s++)
if((s>>i&1) && !(s>>(i+1)&1))
add(dp[w][s^z(i)^z(i+1)],dp[w][s]);
//delete the last one
for(int s=0;s<z(n1);s++)
add(dp[w][s],dp[w][s|z(n1)]);
if(t>m) break;
//to next
for(int s=0;s<z(n1);s++) if(dp[w][s])
{
int ts=0,c=0,x=dp[w][s];
if(t<=n) ts=1,c++;
for(int i=0;i<n1;i++) if(s>>i&1)
ts|=z(d[i]),c++,x=x*W[t-1][i]%MOD;
if(__builtin_popcount(ts)!=c) continue;
add(dp[w^1][ts],x);
}
}
printf("%lld\n",dp[m&1][0]*qkpow(po,n)%MOD);
}
标签:,leq,int,tt,read,dp,MOD 来源: https://www.cnblogs.com/C202044zxy/p/16463153.html
本站声明: 1. iCode9 技术分享网(下文简称本站)提供的所有内容,仅供技术学习、探讨和分享; 2. 关于本站的所有留言、评论、转载及引用,纯属内容发起人的个人观点,与本站观点和立场无关; 3. 关于本站的所有言论和文字,纯属内容发起人的个人观点,与本站观点和立场无关; 4. 本站文章均是网友提供,不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属;如您发现该文章侵犯了您的权益,可联系我们第一时间进行删除; 5. 本站为非盈利性的个人网站,所有内容不会用来进行牟利,也不会利用任何形式的广告来间接获益,纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。
