AGC002F Leftmost Ball
给你 \(n\) 种颜色的球,每个球有 \(k\) 个,把这 \(n\times k\) 个球排成一排,把每一种颜色的最左边出现的球涂成白色(初始球不包含白色),求有多少种不同的颜色序列,答案对 \(10^9+7\) 取模。
将这 \(n\times k\) 个球看成 \(n\) 个白球和 \(n\times k - n\) 个其他颜色的球,由于白球是每种颜色的第一个,所以要保证对于每个位置前缀白球个数均大于等于其他颜色种类数。
设 \(f_{i,j}\) 表示已经放了 \(i\) 个白球和 \(j\) 个其他球的方案数 \((i\ge j)\)。
转移时考虑最后一个放的什么:
-
白球:\(f_{i-1,j}\)
-
新的颜色:\(f_{i,j-1}\times (n-j+1) \times \binom{n\times k-i-(j-1)\times(k-1)-1}{k-2}\)
这里,我们将每个颜色的球的贡献全算上,在剩下 \(n-j+1\) 个颜色中任选一个放在 \(i\),然后该颜色还剩 \(k-2\) 个球,放在后面 \(n\times k-i-(j-1)\times(k-1)-1\) 个空中。
AGC001E BBQ Hard
有 \(n\) 个数对 \((a_i,b_i)\),求出
\[\sum_{i=1}^{n}\sum_{j=i + 1}^{n}{a_i+b_i+a_j+b_j \choose a_i+a_j} \]答案对 \(10^9+7\) 取模
\(2\le n \le 200000,1\le a_i,b_i\le 2000\)
观察到 \(n\) 很大而值域很小,考虑对值域进行操作。
\(\binom{a_i+b_i+a_j+b_j}{a_i+a_j}\) 这个形式其实就是在坐标系上从 \((-a_i,-b_i)\) 只能向上或向右走,走到 \((a_j,b_j)\) 的方案数,所以我们就是要求任意两点间路径方案数的和。
考虑如何把复杂度降下来,如果能对每个点算其他所有点到它的路径方案数,就可以 \(O(n)\) 枚举了。
设 \(f_{i,j}\) 表示所有关键点到 \((i,j)\) 的方案数之和,转移也很简单 \(f_{i,j} = f_{i-1,j}+f_{i,j-1}\),初值 \(f_{-a_i,-b_i}=1\)。
但题目要求 \(i<j\),所以减掉 \(\binom{a_i+b_i+a_i+b_i}{a_i+a_i}\) 后除以 \(2\) 即可。
ARC074C RGB Sequence
有一个序列 \(\left\{a_{i}\right\}\),要给序列中的每个元素一种颜色:红/绿/蓝。有 \(M\) 条限制 \((l,r,x)\),表示格子 \([l,r]\) 中颜色的种数要恰好为 \(x\),问可行的方案数,答案对 \(10^9+7\) 取模。
\(1\le n,m\le 3000\)
观察到只有三种颜色,所以可以记录下每个颜色最后出现的位置。
设 \(f_{i,j,k}\) 表示考虑到第 \(i\) 个数,另外两种颜色最后出现在 \(j\) 和 \(k\),钦定 \(j>k\),转移很显然
- \(f_{i+1,j,k}+=f_{i,j,k}\)
- \(f_{i+1,i,k}+=f_{i,j,k}\)
- \(f_{i+1,i,j}+=f_{i,j,k}\)
对于限制,挂到 \(r\) 上,在每次向后转移前更新一遍,由于已经知道了另外两个颜色最后的位置,就可以得到 \([l,r]\) 中的颜色数了,将不合法的改为 \(0\) 即可。
P2501 [HAOI2006]数字序列
给定一个长度为 \(n\) 的序列 a,求最少需要改变多少个数才能让 \(a\) 单调严格上升,同时每个数改变的绝对值之和最小是多少。
\(1\le n\le 3.5\times 10^4,1\le a_i\le 10^5\)
第一问
考虑保留最多的数,对于 \(i<j\),如果 \(a_i,a_j\) 可以保留,那么至少 \(a_j-a_i\ge j-i\),也就是 \(a_i-i\le a_j-j\)。
设 \(b_i=a_i-i\),其最长不下降子序列即为答案。
第二问
在第一问的基础上,找到两个在 \(b\) 的最长不下降子序列上相邻的点 \(i,j\),那么 \(\forall k \in (i,j),b_k<a_i 或 b_k>b_j\),我们要把中间的这部分改成合法的,不难想到最优情况下一定是前一部分改成 \(b_i\),后一部分改成 \(b_j\),这个中间点直接枚举是可以过的(
同时 dp 记录一下 \(f_i\) 表示 \([1,i]\) 都合法的最小代价即可。
P3943 星空
有一串长为 \(n\) 的灯泡,其中有 \(k\) 个灯是关的。给定 \(m\) 个可以翻转的长度,也就是每次可以翻转这 \(m\) 个长度之一的灯泡,求最少操作多少次可以将所有灯泡打开。
\(n \le 40000, m\le 64,k\le 8\)
将灯的开关状态看为 \(0/1\),每次操作都是让一段区间异或 \(1\)。这种区间操作可以利用差分,这样每次操作修改两个位置。
由于最多有 \(8\) 个灯是关着的,所以差分数组中最多有 \(16\) 个 \(1\),我们要把这些 \(1\) 都改成 \(0\),预处理出相邻两个之间的距离状压 dp 即可。
具体来说,先 bfs 求出想改变两个相距 \(x\) 的位置的状态最少需要操作几次,然后转移时枚举最后修改的两个位置。
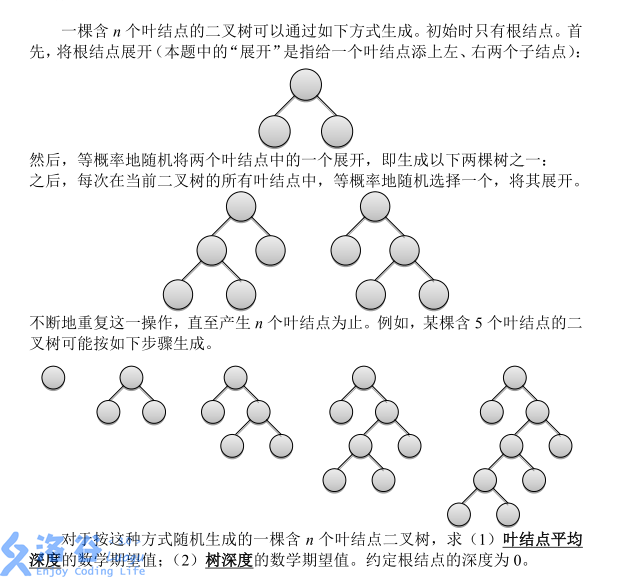
P3830 [SHOI2012]随机树
\(2\le n\le 100\)
第一问
比较简单,设 \(f_i\) 表示 \(i\) 个点的树的叶节点平均深度的期望,转移
\[f_i=\dfrac 1 x(f_{i-1}\times (i-1)+f_{i-1}+2)=f_{x-1}+\dfrac 2 x \]第二问
设 \(f_{i,j}\) 表示有 \(i\) 个叶子,深度 \(\ge j\) 的概率,转移时枚举左儿子叶子数
\[f_{i,j}=\dfrac{1}{i-1}\sum_{k=1}^{i-1}f_{k,j-1}+f_{i-k,j-1}-f_{k,j-1}\times f_{i-k,j-1} \]只要有一边深度 \(\ge j-1\) 就行了,减掉两边都 \(\ge j-1\) 的,至于左子树的大小 \(k\),取 \([1,i-1]\) 的概率都是相等的,所以直接除以 \(i-1\)。
P3058 [USACO12NOV]Balanced Cow Breeds G/S
给一个只有左右括号的字符串,然后用
H、G两种字符来标记这个序列,所有标记H的括号可以组成一个正确的括号序列,所有G标记的括号也组成一个正确的括号序列,然后输出这种标记方案的总数 \(\bmod 2012\) 的值。
由于有两个标记,考虑分开记录,设 \(f_{i,j,k}\) 表示到第 \(i\) 个字符,打 H 标记的剩下 \(j\) 个 "(",打 G 标记的剩下 \(k\) 个 "(" 的方案数。
转移时判断是什么括号,然后分讨打 H 或 G 标记
- 如果是 "("
H: \(f_{i,j,k}+=f_{i-1,j-1,k}\)G: \(f_{i,j,k}+=f_{i-1,j,k-1}\)
- 如果是 ")"
H: \(f_{i,j,k}+=f_{i-1,j+1,k}\)G: \(f_{i,j,k}+=f_{i-1,j,k+1}\)
最后答案为 \(f_{n,0,0}\),第一维可以滚动。
P4798 [CEOI2015 Day1]卡尔文球锦标赛
数位 dp
如果使用 dfs 写法,记忆化数组空间需要 \(O(n^2)\),记录当前在第几位,以及前面填的数中最大是多少,但很可惜空间开不下,放个代码
Code
int dfs(int cur, bool lim, int pre)
{
if(cur == n + 1) return 1;
if(!lim && ~f[cur][pre]) return f[cur][pre];
int res = 0, up = lim ? a[cur] : pre + 1;
for(int i = 1; i <= up; i++)
res = add(res + dfs(cur + 1, lim & (i == up), max(pre, i)));
if(!lim) f[cur][pre] = res;
return res;
}
考虑递推,用时间换空间,设 \(f_{i,j,0/1}\) 表示前 \(i\) 个数,最大值为 \(j\),是否顶着上界的方案数。
转移时从 \(f_{i,j,0/1}\) 向后转移,讨论最后一个填什么
\[f_{i+1,j,0}+=f_{i,j,0}\times j+f_{i,j,1}\times (a_{i+1}-1) \\ f_{i+1,j+1,0}+=f_{i,j,0} \\ f_{i+1,j,1}+=f_{i,j,1}\ (a_{i+1}\neq j+1) \\ f_{i+1,j+1,1}+=f_{i,j,1}\ (a_{i+1}=j+1) \]第一维可以滚动。
AT2087 Friction
给定一个 \(n\times m\) 的矩阵,矩阵上每个格子都有一个小写字母表示颜色,每次操作可以选择一列向下推一格,然后最下面的格子会消失,操作一次的代价为操作前这一列中与旁边格子颜色相同的对数。
求将整个矩阵全消掉所需要的最小代价。
\(1\le n \le 300,2\le m\le 300\)
首先有个性质,任意相邻的两列的代价相互独立,也就是相邻两列的贡献可以单独算。
证明:考虑消掉三列的代价,相邻两列间相对操作顺序是不受第三列的影响的,并且两列如果不相邻是不会产生贡献的,所以代价可以单独计算。
接下来就是简单 dp 了,设 \(f_{i,j}\) 表示第一列还剩 \(i\) 个格子,第二列还剩 \(j\) 个格子消完的代价。
\[f_{i,j}=min(f_{i-1,j},f_{i,j-1})+w(i,j) \]其中 \(w(i,j)\) 表示这个状态下的代价,可以递推出来,假设当前在算第 \(x\) 列和第 \(y\) 列的贡献
\[w(i,j)=w(i-1,j-1)+[s_{i,x}==s_{j,y}] \]于是就可以 \(O(n^2m)\) dp 了。
CF327E Axis Walking
给你一个长度为 \(n\ (1\le n\le 24)\) 的正整数序列 \(S\),再有 \(k\ (0\le k\le 2)\) 个正整数。
求有多少种 \(S\) 的排列方式使得其前缀和不会成为那 \(k\) 个数里的任意一个。 答案对 \(10^9+7\) 取模。
看到 \(n\le 24\) 不难想到状压,设 \(f(S)\) 表示当前已经确定的数为 \(S\),转移时枚举一个没有在 \(S\) 中的数 \(i\),并判断 \(sum(S)+a_i\) 是否合法。
这样复杂度是 \(O(2^nn)\),理论上 3s 是能过的,但是由于这是远古 CF 题,时限减半没能卡过去,考虑换一种转移方式。
对于一个状态 \(S\),我们可以枚举最后一个数是多少,然后从前面的状态转移过来,这个可以用 \(lowbit\) 优化,常数极小,可以通过。
P3451 [POI2007]ATR-Tourist Attractions
给出一张有 \(n\) 个点 \(m\) 条边的无向图,每条边有边权。
你需要找一条从 \(1\) 到 \(n\) 的最短路径,并且这条路径在满足给出的 \(g\) 个限制的情况下可以在所有编号从 \(2\) 到 \(k+1\) 的点上停留。
每个限制条件形如 \(r_i, s_i\),表示停留在 \(s_i\) 之前必须先在 \(r_i\) 停留过。
注意停留不等于经过。
\(2\le n\le2\times10^4\)
\(1\le m\le2\times10^5\)
\(0\le k\le\min(20, n-2)\)
\(2\le r_i, s_i\le k+1, r_i\not=s_i\)
观察到 \(k\) 很小,依然可以状压,所以思路就很清晰了
先对这 \(k\) 个点跑一遍最短路,设 \(f_{S,i}\) 表示从 \(1\) 出发,已经在 \(S\) 中的点停留过,最后待在 \(i\) 的最短路,转移时枚举不在 \(S\) 中的 \(j\),要先判断能否在 \(j\) 停留,这个对每个点存一个需要的状态即可。
这样做空间复杂度是 \(O(2^nn)\) 的,大概是 80MB 左右,并不能过,需要卡空间。
其实差的并不多,只需要把 \(i\) 在 \(S\) 中去掉,也就是当前在 \(i\) 节点,那么状态里就不要存是否有 \(i\),这样空间就是 \(O(2^{n-1}n)\) 了。
标签:le,颜色,好题,times,枚举,序列,转移,dp 来源: https://www.cnblogs.com/acestar/p/16436147.html
本站声明: 1. iCode9 技术分享网(下文简称本站)提供的所有内容,仅供技术学习、探讨和分享; 2. 关于本站的所有留言、评论、转载及引用,纯属内容发起人的个人观点,与本站观点和立场无关; 3. 关于本站的所有言论和文字,纯属内容发起人的个人观点,与本站观点和立场无关; 4. 本站文章均是网友提供,不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属;如您发现该文章侵犯了您的权益,可联系我们第一时间进行删除; 5. 本站为非盈利性的个人网站,所有内容不会用来进行牟利,也不会利用任何形式的广告来间接获益,纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。