可持久化线段树
可持久化线段树 就是 可以持久化的线段树。(??????
大部分可持久化线段树其实都是「可持久化权值线段树」,也就是「主席树」。
这个东西我好像只理解了一点点皮毛啊,暂时先发出来=_=
随便编的例题
你需要维护一个序列 \(a\),初始为空。有 \(n\) 次操作:
1 x:向序列 \(a\) 末尾插入一个数 \(x\)。2 p l r:查询序列中 \(a[1\cdots p]\) 这些数中,值在 \([l,r]\) 内的元素有多少个。强制在线。
\(1\le n\le 2\times 10^5,1\le x\le 2\times 10^5,1\le l\le r\le 2\times 10^5\)。
如果我们查询的是全局值在 \([l,r]\) 内的元素个数,那么可以用线段树来维护。
具体来说,设 \(m=2\times 10^5\),我们可以在 \([1,m]\) 上开一棵权值线段树;插入一个数 \(x\) 就相当于在 \(x\) 这个位置上 \(+1\),查询值在 \([l,r]\) 内的元素个数就相当于求一个区间和。
但是现在要查询只有前 \(p\) 个数,并非全局中的数,怎么办呢
一个想法是我们直接在每次插入的时候,将当前的线段树 copy 一份,保存在 \(\texttt{Tree[i]}\) 中,然后再执行修改。对于查询 2 p l r,我们就直接在 \(\texttt{Tree[p]}\) 上进行查询。然而这样做空间会达到 \(O(m\cdot V)\),直接爆炸。
仔细思考一下每次修改之后线段树的变化:由于我们每次只做了一次单点修改,因此树上发生改变的节点只有 \(x\) 所对的叶子结点到根的这一条路径上的节点。而树高为 \(O(\log m)\),故这部分的节点一共只有 \(O(\log m)\) 个。
这启发我们可以考虑以下的算法:使用动态开点的线段树,每次单点更新的时候,设当前的根节点为 \(\text{rt}\),建立一个新的根节点 \(q\);从 \(q\) 一路往下走,如果修改的位置在 \(\text{rt}\) 的左子树,那么将 \(q\) 的左子节点指向更新后的 \(\text{rt}\) 的左子树,同时右子树直接指向 \(\text{rt}\) 的右子树,然后让 \(q\) 和 \(\text{rt}\) 同时往左子节点的方向走。如图所示:
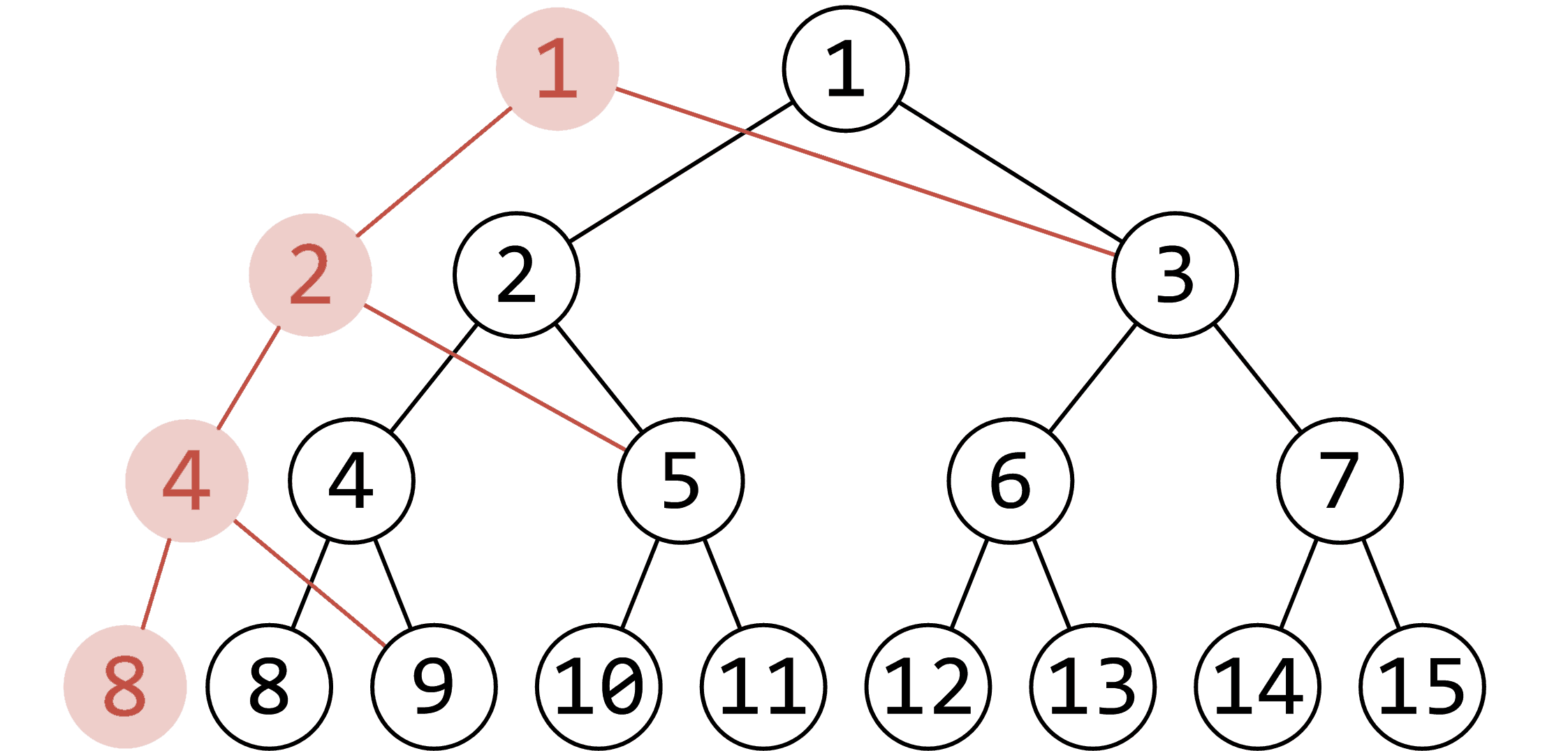
//d[p].val 维护的是 p 对应区间内的数的个数。
inline void pushup(int p){
d[p].val=d[ls(p)].val+d[rs(p)].val;
}
inline int insert(int x,int ql,int qr,int o){
int p=++tot;d[p]=d[o];
if(ql==qr){d[p].val++;return p;}
int mid=(ql+qr)>>1;
if(x<=mid)d[p].ls=insert(x,ql,mid,lson(o));
if(x>mid)d[p].rs=insert(x,mid+1,qr,rson(o));
pushup(p);
}
//在主函数中:
root[++cnt]=insert(x,1,V,root[cnt-1]);
静态区间第 k 小
给定一个长为 \(n\) 的序列,有 \(q\) 次询问。每次询问给出 \(l,r,k\),你需要求出区间 \([l,r]\) 内的第 \(k\) 小数。
数据范围:\(1\le n,q\le 2\times 10^5\)。
之前我们用整体二分切了这个题,虽然口胡了一个 \(O((n+q)\log n)\) 的做法,但是实际实现的时候为了方便,写的仍然是 \(O((n+q)\log^2n)\) 的 2log 做法。这里我们介绍一个好写的 1log 在线算法:可持久化权值线段树。
可以发现,套用上题的方法,我们可以在 \(O(\log n)\) 的时间内求出 \([1,r]\) 内 \(\le x\) 的数的个数与 \([1,l-1]\) 内 \(\le x\) 的数的个数,于是在外面再套一层二分就得到了一个憨憨 2log 做法。
实际上完全不需要外面那一层二分,我们可以直接在线段树上二分!代码如下:
inline int query(int q,int p,int ql,int qr,int k){
if(ql==qr)return ql;
int mid=(ql+qr)>>1,cnt=d[ls(q)].val-d[ls(p)].val;//cnt 即为左子树内 <=k 的元素个数。
if(k<=cnt)return query(ls(q),ls(p),ql,mid,k);
else return query(rs(q),rs(p),mid+1,qr,k-cnt);
}
//在主函数中
ans=query(root[l-1],root[r],1,V,k);
这样做的复杂度是 \(O(\log n)\) 的。如果要支持修改,还需要再套一层树状数组,不如直接整体二分。
题目选讲
LuoguP2633 Count on a Tree Past 5
板子题。
我们可以对每个 \(u\) 维护出来 \(1\to u\) 路径上节点构成的权值线段树,然后求第 \(k\) 大就直接类似上面的做法,二分就行了。需要求出来的节点就是 \(u,v,\text{LCA}(u,v),\text{Father}(\text{LCA}(u,v))\)。
时间复杂度 \(O((n+m)\log n)\)。AC Code
LuoguP3293 SCOI2016 美味 Present 6
如果没有那个 \(+x_i\) 那么就是一个 \(\text{01-Trie}\) 板子题。
我们思考 \(\text{01-Trie}\) 求异或极值时本质是什么:从高位往低位找,每次贪心地尽可能让当前这一位是 \(1\)。
那么仍然考虑这样的思路:对于一个询问 \(b_i\),我们假设当前是第 \(r\) 位,那么想让这一位上是 \(1\),就相当于是这段区间内要存在一个在 \([S,S+2^r)\) 内的数。其中 \(S\) 是当前已经累积出来的数值。
那么现在要 \(+x_i\) 就相当于询问是否有 \([S-x_i,S+2^r-x_i)\) 内的数。用之前讲的主席树维护一下就行了。
从这个方面来看,\(\text{01-Trie}\) 本质上就是动态开点的,未离散化的权值线段树。
这句话是我半年前在某个群听到的,当时我比较萌萌还跟人家对线,现在看来确实是这么一回事qwq
我们这么做的时间复杂度是 \(O(\log ^2V)\),比普通的 \(\text{01-Trie}\) 多了一个 \(\log\)。这是因为有了 \(+x_i\) 的限制后,我们没有办法每次直接通过看左右子树内的值来确定是否存在符合条件的值了,而是要重新拆成 \(O(\log V)\) 个区间合并起来。这里 \(V=10^5\) 为值域。
\(\text{01-Trie}\) 能砍掉这一个 \(\log\) 是因为它直接把值域补全成了 \(2\) 的幂,从而建出了一棵完全二叉树。这样一来,每个节点对应的区间长度也就变成了 \(2\) 的幂,恰好对应上了二进制中的一位。
LuoguP3567 POI2014 KUR-Couriers Present 5
考虑找出来 \([1,l-1]\) 的权值线段树与 \([1,r]\) 的权值线段树。
那么两个儿子中如果有一个满足:这两棵线段树上的对应值相减 \(\ge(r-l+1)/2\),答案就有可能在这个子树内。
不断往下递归就行了。如果发现左右儿子都不满足就说明不行。复杂度 \(O((n+m)\log n)\)。AC Code
为什么数据不卡 2log 的随机化啊QAQ
LuoguP2839 middle Future 7.5
对于最大化中位数,一个常见的套路是二分答案:设答案为 \(m\),把 \(\ge m\) 的数设为 \(1\),\(<m\) 的数设为 \(-1\),然后相当于要找到一个区间使得其区间和 \(\ge 0\)。
到这里你或许会想到整体二分,但是经过一番思考后我发现我并不会这题的整体二分做法=_=
而且他还强制在线。。那显然必须要用在线算法了qwq
我们对于每次询问做一个二分,现在要求的就是:左右端点分别在 \([a,b],[c,d]\) 区间内,且 \(\ge m\) 的数权值为 \(1\),\(<m\) 的数权值为 \(-1\) 时的最大区间和。
不难发现,对于一个确定的 \(m\),我们可以扫一遍整个序列,然后标记一下,再用线段树维护一个类似区间最大子段和的东西做到 \(O(\log n)\) 单次查询。然后设值域为 \(V\) 就需要开 \(V\) 棵线段树,显然空间根本开不下。
其实完全没有必要开这么多:先离散化,然后注意到每次值域上加一的时候实际上均摊下来只有 \(O(1)\) 个位置的权值会发生改变。因此,第 \(i\) 棵线段树和第 \(i+1\) 棵线段树只有 \(O(1)\) 条链是不同的。
因此可以用类似可持久化线段树的操作,提前预处理出来这些线段树,然后就做完了。AC Code
LuoguP4137 Rmq Problem / mex Present 6
可持久化线段树维护区间 \(\text{mex}\) 的套路。考虑如何判断答案是不是 \(x\)。
若区间 \([l,r]\) 内的 \(\text{mex}=x\),需要满足:
- \(0,1,\cdots,x-1\) 都在 \([l,r]\) 内出现过。
- \(x\) 没有在区间 \([l,r]\) 内出现过。
我们都知道可持久化线段树可以快速判断一个数是否在区间内出现过,但是如果你暴力判断 \(x\) 次显然是不行的。
考虑建立一棵权值线段树,线段树上叶节点 \(v\) 位置维护的是数 \(v\) 在序列中最后一次出现的位置(若不存在则为 \(0\)),那么只要线段树中 \([0,x-1]\) 内的最小值 \(\ge l\),就说明这些数在 \([l,n]\) 中都出现过。
这启发我们用线段树维护区间最小值,同时查询的时候在线段树上二分,这样就可以做到 \(O(\log n)\) 了。
怎么判断这些数 \(r\) 之前出现过呢?其实很简单,建出 \(n\) 棵线段树,第 \(i\) 棵线段树维护前缀 \([1,i]\) 的信息即可。
可持久化一下就做到了 \(O(n\log n)\) 的时空复杂度。
由于本题不强制在线,我们可以将询问按照右端点排序,从而省掉可持久化。AC Code
CF1436E Complicated Computations Future 7.0
考虑依次枚举 \(x=1,2,\cdots,n\),判断是否有一个区间的 \(\text{mex}=x\)。
那么第一个使判断结果为否的 \(x\) 就是我们要求的答案。
如何判断是否有一个区间的 \(\text{mex}=x\) 呢?仍然考虑这两个条件:
- \(1,2,\cdots,x-1\) 都在该区间内出现过。(本题中 \(\text{mex}\) 与上题不太一样,\(0\) 是不算的)
- \(x\) 没有在区间 \([l,r]\) 内出现过。
为了满足第二个条件,我们把序列中的 \(x\) 都找出来,用这些 \(x\) 将序列分为许多段,那么要求的区间必须在一段内。
现在我们已经可以确定这些区间的 \(\text{mex}\) 不超过 \(x\) 了,那么只要让区间内的 \(\text{mex}\) 尽可能大就好了。这样一来,区间的长度显得越长越好,也就是说,最优情况下应当直接将区间取满刚才分出的一整段。
使用可持久化线段树查询 \(\text{mex}\) 即可。显然这里无法离线。
设 \(x\) 的出现次数为 \(c_x\),则查询 \(\text{mex}\) 的次数为 \(O(\sum c_x+1)=O(n)\),故总的复杂度为 \(O(n\log n)\)。
标签:le,持久,log,int,text,线段,区间 来源: https://www.cnblogs.com/YunQianQwQ/p/16294895.html
本站声明: 1. iCode9 技术分享网(下文简称本站)提供的所有内容,仅供技术学习、探讨和分享; 2. 关于本站的所有留言、评论、转载及引用,纯属内容发起人的个人观点,与本站观点和立场无关; 3. 关于本站的所有言论和文字,纯属内容发起人的个人观点,与本站观点和立场无关; 4. 本站文章均是网友提供,不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属;如您发现该文章侵犯了您的权益,可联系我们第一时间进行删除; 5. 本站为非盈利性的个人网站,所有内容不会用来进行牟利,也不会利用任何形式的广告来间接获益,纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。
