标签:Formulas Determinant end 公式 begin 余子式 vmatrix 行列式 2.6
行列式公式和代数余子式
reference的内容为唯一教程,接下来的内容仅为本人的课后感悟,对他人或无法起到任何指导作用。
Reference
- Course website: Determinant Formulas and Cofactors | Unit II: Least Squares, Determinants and Eigenvalues | Linear Algebra | Mathematics | MIT OpenCourseWare
- Course video: 【完整版-麻省理工-线性代数】全34讲 配套教材_哔哩哔哩_bilibili
- Course summary: Lecture 19: Determinant formulas and cofactors (mit.edu)
这一节我感觉可以稍稍快进了,因为我第一次学就是直接从行列式的代数余子式公式开始背,然后推行列式的各个性质,由于这样十分痛苦,我不得不强行记住了代数余子式,以至于回过头来看这部分竟然是我最熟悉的部分了...
行列式只是线性代数中很小的一个部分,分支罢了,不应该放到第一章直接给人打击!
Big Formula
行列式可以由三个基本性质完备定义:
- 单位阵行列式为 1
- 互换两行, 行列式变号
- 行列式对每一行具有单独的线性性质 (倍乘, 加和)
2 × 2 & 3 × 3
首先分析 2×2 矩阵, 根据三个基本性质很容易推出行列式公式:
\[\begin{align*} \begin{vmatrix} a & b\\ c & d\\ \end{vmatrix} &= \begin{vmatrix} a & 0\\ c & d\\ \end{vmatrix}+ \begin{vmatrix} 0 & b\\ c & d\\ \end{vmatrix}\\ &=(\begin{vmatrix} a & 0\\ 0 & d\\ \end{vmatrix}+ \begin{vmatrix} a & 0\\ c & 0\\ \end{vmatrix})+ ( \begin{vmatrix} 0 & b\\ c & 0\\ \end{vmatrix}+ \begin{vmatrix} 0 & b\\ 0 & d\\ \end{vmatrix})\\ &=\begin{vmatrix} a & 0\\ 0 & d\\ \end{vmatrix}+\begin{vmatrix} 0 & b\\ c & 0\\ \end{vmatrix}\\ &=\begin{vmatrix} a & 0\\ 0 & d\\ \end{vmatrix}-\begin{vmatrix} b & 0\\ 0 & c\\ \end{vmatrix}\\ &=ad-bc \end{align*} \]我们通过先对第一行进行拆解,得到两个行列式的和。再对两个行列式的第二行进行拆解,得到了 2*2=4 个行列式的和,这里面有两个出现全零行,只有两个行列式有值 (因为行交换一定会出现对角阵), 然后我们分析交换了几次判定奇偶即可.
同理 3×3 也是这个道理, 先对第一行拆解, 再对第二行拆解, 最后拆到第三行, 所以一共有 33 个行列式, 其中每行只有一个元素, 因此如果想让列不出现全零, 每一列也必须只能有一个元素, 也就是说第一行选完的列第二行不能再选了, 因此有 3! 种组合. 其实这相当于置换, 置换也是 3! 个.
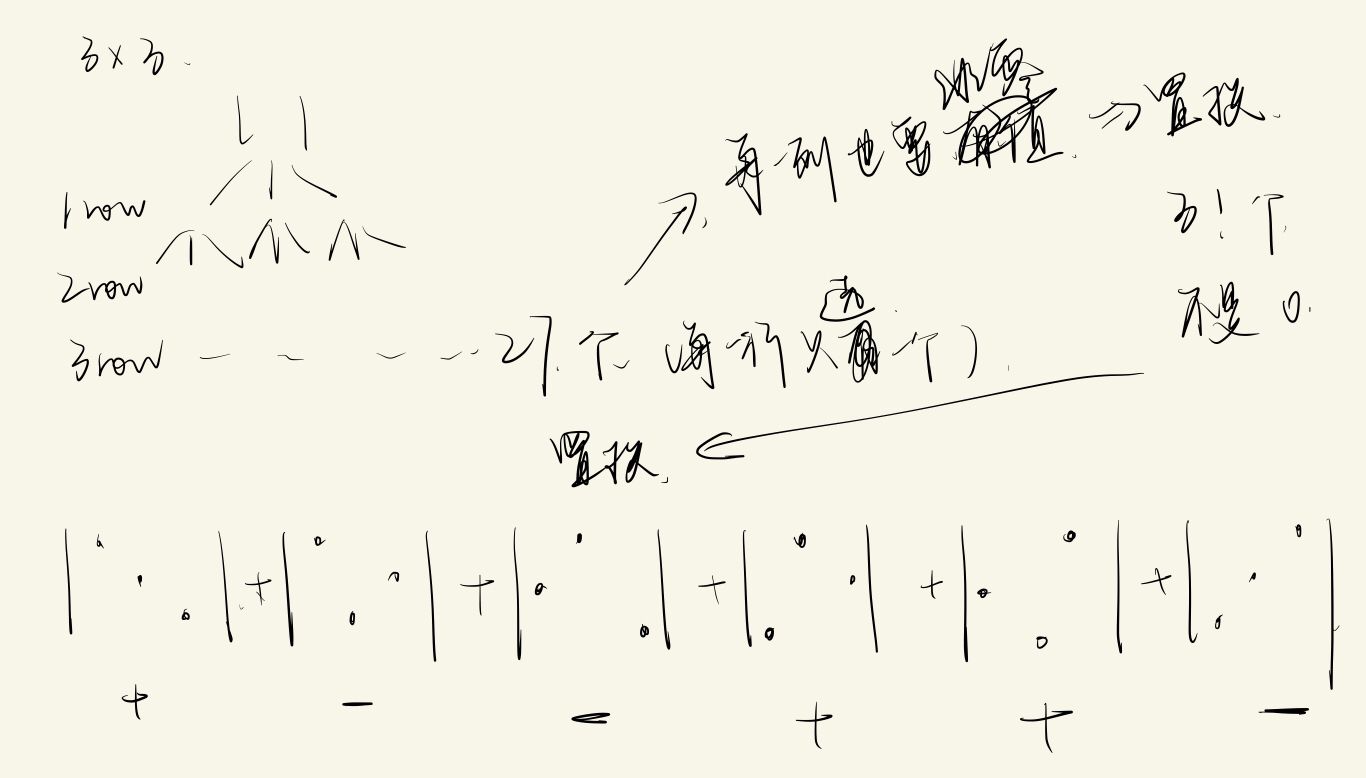
设矩阵为 A, 元素为 aij, 则行列式为:
\[a_{11}a_{22}a_{33}-a_{11}a_{23}a_{32}+a_{12}a_{23}a_{31}-a_{12}a_{21}a_{33}+a_{13}a_{21}a_{32}-a_{13}a_{22}a_{31} \]n × n
于是我们可以归纳任意矩阵的行列式了
\[\det\boldsymbol{A}=\sum_{n! \text{ terms}}\pm a_{1\alpha }a_{2\beta }\cdots a_{n\omega } \]其中 \((\alpha, \beta, \cdots, \omega)\) 为 \((1, 2, \cdots, n)\) 的置换.
Example 1
相对来说最简单的行列式求法仍然是消元法, 不过上面的公式有时也能为求解行列式带来方便. 比如:
\[\begin{vmatrix} 0 &0 &1 &1 \\0 &1 &1 &0 \\1 &1 &0 &0 \\1 &0 &0 &1 \end{vmatrix}= \begin{vmatrix} 0 &0 &0 &1 \\0 &0 &1 &0 \\0 &1 &0 &0 \\1 &0 &0 &0 \end{vmatrix}+ \begin{vmatrix} 0 &0 &1 &0 \\0 &1 &0 &0 \\1 &0 &0 &0 \\0 &0 &0 &1 \end{vmatrix} \]如果采用消元法很难一眼看出来结果, 但是有了上面的式子我们就知道只有这两种矩阵才可能非零, 其余矩阵必然出现列全零的情况, 这两个是仅有的置换. 左面的需要交换 1,4 和 2,3 行, 右面只需要交换 1,3 行, 所以符号相反, 行列式为零.
所以这个矩阵不可逆, 因为第一列+第三列=第二列+第四列.
Cofactor Formula
我实在懒得介绍 代数余子式 (Cofactor) 和 余子式 (Minor) 了, 如果学了一遍线代一定知道这是什么了. Lecture 中从 3阶行列式的公式开始讨论, 得到代数余子式的概念.
\[\det\boldsymbol{A}=a_{i1}C_{i1}+a_{i2}C_{i2}+\cdots+a_{in}C_{in},\quad C_{ij}=(-1)^{i+j}M_{ij} \]这是按行展开的, 由于转置行列式不变, 因此按列展开的也可以写成类似的形式, -1 的乘幂仍然为 i+j.
Example 2
懒得写了, 直接看图, 就是一个利用递推的行列式...

Summary
行列式公式, 就是一个烦人的公式, 老实说我不知道用一些奇淫技巧求一些行列式能有什么用, 也不知道能从这个公式看出些什么东西来, 大概就是锻炼智商吧... 结果学一圈发现求行列式真的没什么用, 但是大一学的时候却搞得很难, 各种奇奇怪怪的行列式和证明要求掌握, 很是痛苦...
标签:Formulas,Determinant,end,公式,begin,余子式,vmatrix,行列式,2.6 来源: https://www.cnblogs.com/wind2375like/p/16145243.html
本站声明: 1. iCode9 技术分享网(下文简称本站)提供的所有内容,仅供技术学习、探讨和分享; 2. 关于本站的所有留言、评论、转载及引用,纯属内容发起人的个人观点,与本站观点和立场无关; 3. 关于本站的所有言论和文字,纯属内容发起人的个人观点,与本站观点和立场无关; 4. 本站文章均是网友提供,不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属;如您发现该文章侵犯了您的权益,可联系我们第一时间进行删除; 5. 本站为非盈利性的个人网站,所有内容不会用来进行牟利,也不会利用任何形式的广告来间接获益,纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。
